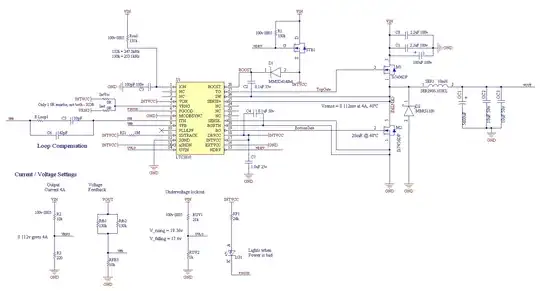
I'm going to answer my own question to consolidate the information. Thanks for the answers that have led me to figure this out. I'm going to spend most of my time answering how to find the values, but the other answers are:
1a) Is it the best way? Pretty much, because: Low component cost and ability to design extremely low current draw so as to deliver as much harvested power to the load as possible.
1b) Is there a simpler method? Yes, some more monolithic ICs for energy harvesting exist that include similar functionality. BUT, they cost more and use a lot more current to achieve the same result.
3) How does the example work? The example is actually wrong. It may still work, but the HYST pin should be connected to REF if you're going to use an external positive feedback network as in the example with that IC.
2) How do you figure out the values? Initially the actual Ohm values are not important. What you want to calculate are the RATIOS of R1 and R2 with relation to R3.
For reference here is your generic voltage comarator ciruit with positive feed back:
simulate this circuit – Schematic created using CircuitLab
Your starting point is to decide on the Vhigh trip point and the hysteresis band (which is just the voltage difference between your high and low trip points). You also need to know what Vref is of course.
Once you have those three values, you're ready to calculate the R1 and R2 ratios. Let R3 = 1 in all the equations as that will give the result as a ratio to R3.
The two formulas we will use are:
$$
\text{High trip point will be: } \left( V_{\operatorname{high}} \right)
\text{ and Hysteresis band will be: } \left( V_{\operatorname{band}} \right)\\
\operatorname{R1} = \operatorname{R3} \left( \frac{V_{\operatorname{band}}}{V_{\operatorname{cc}}} \right)
\text{ and }
\operatorname{R2} = 1 \left/ \left(
\frac{V_{\operatorname{high}}} {V_{\operatorname{ref}} \times \operatorname{R1}}
- \frac{1} {\operatorname{R1}}
- \frac{1} {\operatorname{R3}}
\right) \right.
$$
Remember that R3 = 1, so we can just drop it completely from the R1 equation. Once you solve those two equations you have the ratio between R1->R3 and R2->R3. Now it's just a matter of selecting a real value for R3 and you can multiply those ratios with the value to get your real vales.
So how to choose R3? There are two considerations, firstly you want it to be a pretty big value so as to use a very low amount of current. But it can't be so large that it doesn't deliver enough current to actually work.
How much current does it need to deliver? That depends on your device, but the values I've seen usually suggest it should deliver Input Bias Current * 10 as a minimum and * 100 is recommended. So if your device had an Input Bias Current of 5nA, you would want R3 to deliver 5uA at the minimum point going with recommended values.
Once you know how much current you want over R3, figuring out its resistance is just a matter of using Ohms law (V=IR). But there are two values for V that it will operate at. It could be at V = Vref or V = Vcc - Vref. You will need to calculate both then select which ever is LOWER.
If we let the current over R3 be called I3, then the two formulas for R3 are:
$$
\operatorname{R3} = V_{\operatorname{ref}} / \operatorname{I3}
\text{ and }
\operatorname{R3} = \left( V_{\operatorname{cc}} - V_{\operatorname{ref}} \right) / \operatorname{I3}
$$
Now that you have R3, it's just a matter of multiplying the ratios you got for R1 and R2 with this value.
Applying this knowledge to the original example, it seems that the values given in it are somewhat off. So let's go over that example and find out what the vales should be.
The example doesn't tell us what Vcc is and if we work backwards from the values that are given, Vcc would need to be 3.21V to give those values. Which doesn't make any sense since the Vhigh trip point was stated as being 3.6V. So let's go with a more sensible value and say Vcc is 4V.
The values we start with are:
$$
\begin{eqnarray*}
V_{\operatorname{cc}} &=& 4\text{v}\\
V_{\operatorname{ref}} &=& 1.182\text{v}\\
V_{\operatorname{high}} &=& 3.6\text{v}\\
V_{\operatorname{band}} &=& 0.4\text{v}\\
\end{eqnarray*}
$$
Now calculate R1 and R2 using the above formulas:
$$
\operatorname{R1} = \frac{0.4}{4} = 0.1\text{, }
\begin{eqnarray*}
\operatorname{R2} &=& 1 \left/ \left(\frac{3.6}{1.182 \times 0.1} - \frac{1}{0.1} - 1 \right) \right.\\
\operatorname{R2} &=& 1 \left/ \left(\frac{3.6}{0.1182} - 10 - 1 \right) \right.\\
\operatorname{R2} &=& 1 \left/ 19.4568 \right.\\
\operatorname{R2} &=& 0.051
\end{eqnarray*}\\
$$
Next we need to determine what the largest value for R3 can be. Looking at the datasheet, the Input Bias (or Input Leakage) has a maximum value of 1nA. Using the *100 rule that means R3 should deliver 1uA at the minimum point.
Calculating the two possible extremes of R3 using R = V/I:
$$
\begin{eqnarray*}
\operatorname{R3} &=& 1.182 / 0.000001 \text{ and } \operatorname{R3} &=& \left( 4 - 1.182 \right)/0.000001\\
&=& 1.18M\Omega &=& 2.81M\Omega\\
\end{eqnarray*}
$$
Finally we multiply the previously calculated ratios with R3 and we get our final values of:
R1 = 118K
R2 = 60K
R3 = 1.18M
Now that is using a very conservative value for R3, we could certainly go bigger which would further reduce the current used by the UVLO. So what would those values be if we went with the original 20Meg for R3? Firstly that would make I3 59.1nA, which is still plenty above the 1nA leakage. So it probably would work just fine, the accuracy might suffer a bit.
With R3 = 20M we would get R1 = 2M and R2 = 1.02M.