The distribution of phase angle between identical zero mean Gaussian random signals?

Question

I am trying to solve the 2013 paper set by ISRO for electrical engineers. I was hoping to get some clues on how to approach this problem - No 22. random signals which have gaussian distributions will not be periodic and I can't understand what they mean by phase difference between the two signals.

Question No 22

If x and y are two random signals with zero mean Gaussian distribution having identical standard deviation, the phase angle between them is

a) Zero mean Gaussian distributed

b) Uniform between \$-\pi\$ and \$\pi\$

c) Uniform between \$\frac{-\pi}{2}\$ and \$\frac{\pi}{2}\$

d) Non zero mean Gaussian distributed

My gut feeling tells me that since both signals are zero mean, it's more likely to spend time at 0 (depending on the standard deviation), so a phase difference of 0 is more likely. So I can rule out Uniform distribution and a non zero gaussian distribution. So I intuit that the answer is (A)

I found a paper which talks on this topic, but it went right above my head. I was hoping for an explanation of what the question is asking and what the answer is and why?

Answer 1

$$\mathcal{X_1}=\mathcal{N}(0,\sigma^2)$$ $$\mathcal{X_2}=\mathcal{N}(0,\sigma^2)$$ $$\theta=\arctan(\mathcal{X_1},\mathcal{X_2})$$

Since arctan ranges from \$-\frac{\pi}{2}\$ to \$-\frac{\pi}{2}\$

there can only be one answer and that is c, you could do the math but the answer is c

These questions are designed to be tricky, simple relationships can save you time if you look at the question as a whole. In this case you need to know what the output of arctan is.

Answer 2

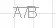
So, let's dig into this.

The question is ambigously asked.

1. Real-Valued interpretation

If the question is meant to read

\$x, y\sim \mathcal N(0,\sigma^2)\$: what is the distribution of \$A= \lvert\angle x-\angle y\rvert\$?

then the answer would be: since \$\angle x = 0 \, \forall x \in\mathbb R\$ (and the same for \$y\$), \$ a = \lvert\angle x-\angle y\rvert = \lvert0-0\rvert = 0\implies f_A(a) = \delta(a)\$.

The only choice that would be correct here would be "a)"; because the Dirac delta is the marginal case of the zero-mean normal distribution with zero variance.

2. Complex-value interpretation

I'm swinging towards this interpretation, because it makes a little more sense.

Likely, however, the question is meant to read

\$x, y\sim \mathcal{CN}(0,\sigma^2)\$: what is the distribution of \$A= \lvert\angle x-\angle y\rvert\$?

(which contradicts the literal text; when you say "normally distributed", you mean the real \$\mathcal N\$, not the circularly complex \$\mathcal {CN}\$)

You'd then realize that the phase of a circularly complex normal variable is uniform between \$0\$ and \$2\pi\$ or between \$-\pi\$ and \$\pi\$ (or, however you define your range of valid angles). It doesn't really matter; all it does in the end translate the PDF.

I'll pick \$\angle x,\angle y\sim \mathcal U(-\pi,\pi)\$ because it allows the PDF to be symmetric, which will be useful when we calculate the following:

\begin{align} \tilde A &= \angle X - \angle Y& \tilde Y = -Y\\ &= \angle X + \angle\tilde Y\\ \implies\\ f_A(a) &= f_{\angle X} * f_{\angle\tilde Y}&*\text{ being the convolution}\\ &= f_{\angle X} * f_{\angle Y} & \text{due to symmetry of Y's PDF}\\ &= \text{rect}(\frac{u}{2\pi})*\text{rect}(\frac{u}{2\pi}) & \text{convolution of two $2\pi$ wide zero-centered rectangles}\\ \end{align}

That's a triangular distribution. If you look at \$f_{\lvert A \rvert}\$, it becomes a linear downslope. None of the options allow a triangular distribution.

3. Interpration as coordinates of point in plane

If the question is meant to read

\$x, y\sim \mathcal N(0,\sigma^2)\$: what is the distribution of \$A=\angle (x,y)\$?

You'd realize that \$(x,y)\sim\mathcal {CN}(0, \frac{\sigma^2}2)\$, and all these zero-mean circularly complex normally distributed variables have uniform phase over a range of \$2\pi$. That'd imply b) is right.

Answer 3

For two sinusoids at the same frequency, but otherwise uncorrelated, the phase difference is in the range \$-\pi \le\ \phi \lt\ \pi\$, and all phase differences in that range are equally probable. Now apply this to the Fourier transforms of the two uncorrelated Gaussian signals and you get a uniform distribution in the range \$-\pi \le\ \phi \lt\ \pi\$