12

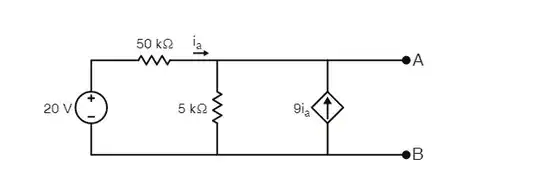
I have a fifth order transfer function for which I designed a controller using pole-zero cancellation technique on a root locus. I am targeting \$<5%\$ overshoot and \$<2s\$ settling time. Currently, the overshoot criteria are satisfied.

Note I know that exact p-z cancellation is nearly impossible in real life.

The controller and the original 5th order transfer function are shown in Simulink below

enter image description here

which give a response with a long tail in the transient response, and thus, a very long settling time.

enter image description here

As per Chu's comment here,

Placing zeros close to poles in an attempt to 'cancel' is not too clever. It's usually impossible to plonk a zero directly on top of a pole and expect both poles and zero to stay put. The result is a 'dipole' (a pole and zero in close proximity) that gives rise to a long-tail in the transient response.

and HermitianCrustacean's comment,

The 4th order controller you've chosen is difficult to numerically model ...

What would be the root cause of this unacceptably long settling time, inexact p-z cancellation (the controller which is difficult to numerically model), or both? Any suggestions on how to improve the response would also be greatly appreciated.

Poles of 5th order system

   Poles =

   1.0e+02 *

  -9.9990 + 0.0000i
  -0.0004 + 0.0344i
  -0.0004 - 0.0344i
  -0.0002 + 0.0058i
  -0.0002 - 0.0058i

Zeros placed to cancel poles

enter image description here

4th order controller

enter image description here

I would be happy to provide further information if needed.

kbakshi314
  • 255
  • 1
  • 12
rrz0
  • 1,171
  • 1
  • 21
  • 42
  • 1
    What is your hysteresis zone? If you've got .1 volt or so at the top to work with, the transient may not matter. – Robert Harvey Jan 12 '19 at 17:25
  • 1
    Thanks for your comment. Hysteresis is 0.0835 which is more than the 2% (0.02 for a step input of 1) criterion for settling time – rrz0 Jan 12 '19 at 17:56
  • Can you upload the Simulink File please? – Brethlosze Jan 21 '19 at 06:00
  • In the real world you go to the mechanical engineer's cube and insist that more sensors and/or actuators are added so that you can treat it as a MISO or SIMO system with no more than three significant modes each. – TimWescott Jan 29 '19 at 21:40
  • 1
    I put this as a comment and not a solution because it's a guess. Try putting four zeros at \$s = -1\$ and see what happens. Then try putting them all at \$s = -4\$. Then see if that suggests a way that you can get things working. Note that (without actually checking), my intuition tells me that the system just isn't going to be terribly robust. – TimWescott Jan 29 '19 at 21:51
  • 2
    One of the ways in which the system is "difficult to model" is that it is difficult to model a pole and zero exactly cancelling. – david Mar 22 '19 at 07:47
  • By doing a derivative sensitivity analysis, you can found out which term is most critical by adjustments of =+/-0.1%. I think it will be the s^2 error tolerance factors that are the root cause of your resonance. A FFT spectrum can also show the critical factors with a Pole Zero plot using Falstad. – Tony Stewart EE75 Jul 23 '19 at 19:06

2 Answers2

3

The slow oscillating behavior in the system results from a pole with real part close to zero and, by looking at your step response, with a frequency close to \$0.1 \; \text{Hz}\$ \$\; (0.62 \; \text{rad/s})\$. So the poles causing it are the ones at \$s_0 = -0.02+0.58i\$ , and \$s_1 = -0.02-0.58i\$.

You should check if they really have been cancelled, and if they have not, try using root locus and different gains to change the pole positions away from the complex axis (having real parts as negative as possible).

jDAQ
  • 2,517
  • 1
  • 9
  • 19
1

I think you need to check the residue corresponding to pole you want to cancel to check if pole-zero cancellation is valid. Residue is the constant multiplied to partial fraction term of this pole. For example, if $$F(s)=\frac{26.25(s+4)}{s(s+3.5)(s+6)}$$ the residue of the partial fraction term of \$s+3.5\$ pole is \$1\$ which cannot be neglected so \$s+3.5\$ and \$s+4\$ cannot cancel each other, and for $$F(s)=\frac{26.25(s+4)}{s(s+4.01)(s+6)}$$ the residue of the partial fraction term of \$s+4.01\$ pole is \$0.033\$ which can be neglected so \$s+4.04\$ and \$s+4\$ can cancel each other.

Reference: Example 4.10, page 195 in Control Systems Engineering, Norman S. Nise, 6th Edition, 2010, John Wiley.

Null
  • 7,448
  • 17
  • 36
  • 48
mohamed ehab
  • 11
  • 2