0

Could you tell me how to find Vd and Vb in the schematic please? Is the PNP in saturation or linear mode?

I found Vb, with Vbe = Vb - Ve, then Vb = Ve -Vbe. To find the mode of the pnp, I need to find Ib, and so Vd. But I don't know how to find it.

Thanks.

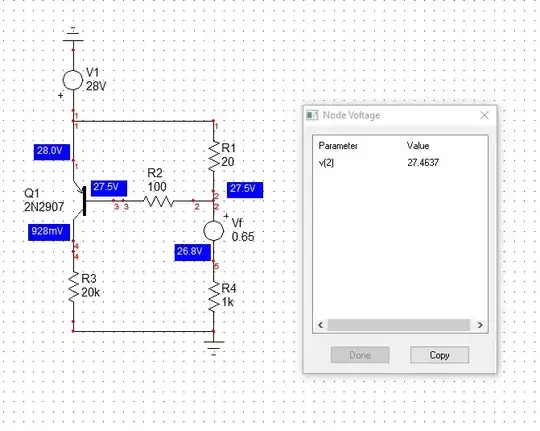
enter image description here

Tack
  • 311
  • 3
  • 13
  • Hello Tack, you need to know the voltage drop across diode \$D_3\$. For this small-signal diode, the \$V_f\$ varies with the current and this current is what you need : ) I am not sure about the level of detail is expected from this exercise but I would replace the diode by a voltage source and solve your circuit. When you write \$V_{be}\$ in your circuit, you also imply a constant value but it is not and it corresponds to the b-e junction voltage drop which also depends on the base current (and temp.) so replacing the diode by a source having a \$V_f\$ value is probably the easiest way to go. – Verbal Kint Jan 11 '19 at 12:45
  • Thank you for your answer Verbal Kint. If we assume that Vf = 0,6 V, how can I find Vd? I can have Vout = Vd-0.6. But I don't find Vd with Vf. – Tack Jan 11 '19 at 13:48

2 Answers2

2

The first thing to do is to redraw the schematic into a somewhat better (more readable) layout. (You can read a short discussion I wrote here.)

schematic

simulate this circuit – Schematic created using CircuitLab

At this point, you don't know whether the collector of \$Q_4\$ is acting like a current source (active mode) or more like a voltage source (somewhere in saturation.) So, some back-of-the-envelope calculations are indicated.

If you assume that \$\mid\, V_{\text{BE}_4}\mid\:=\:\mid\,V_{\text{D}_3}\mid\,=700\:\text{mV}\$. Then \$V_B\approx 27.3\:\text{V}\$ and \$V_D\approx V_A+700\:\text{mV}\$. So:

$$\begin{align*} \frac{V_D}{R_1}+\frac{V_D}{R_2}+\frac{V_D-700\:\text{mV}}{R_4}&=\frac{28\:\text{V}}{R_1}+\frac{28\:\text{V}-700\:\text{mV}}{R_2} \end{align*}$$

Which can easily be solved for \$V_D\$. If you do that, you'll find that there is enough base current in \$Q_4\$ to, by itself and with only \$\beta_4=1\$, the collector current would be sufficient to drive \$Q_4\$ into early saturation.

At first blush, from this we can conclude that \$Q_4\$ is saturated -- probably deeply so. Therefore \$V_C\ge 28\:\text{V}-200\:\text{mV}\$. Also, that base current would suggest that the assumption, \$\mid\, V_{\text{BE}_4}\mid\:=700\:\text{mV}\$, is probably close.

If \$Q_4\$ is saturated, then the collector will look more like a voltage source, so it's pretty easy to compute the current in \$R_3\$, if you want it. Also, the current in \$D_3\$ can be easily estimated now that \$V_D\$ is known. If you want to double-check the voltage drop estimate for \$D_3\$ you'll have to check this estimated current against the datasheet. (But the slight adjustments you make probably won't significantly alter the current computations -- perhaps a few hundred microamps of difference?)

You could set up nodal equations like the following (only started out, for now):

$$\begin{align*} \frac{V_A}{R_4}&=I_{D_3}\\\\ \frac{V_B}{R_2}&=I_{B_4}\\\\ \frac{V_C}{R_3}&=I_{C_4}\\\\ \frac{V_D}{R_1}+\frac{V_D}{R_2}+I_{D_3}&=\frac{28\:\text{V}}{R_1}+\frac{V_B}{R_2} \end{align*}$$

But then you'd have to substitute in the Shockley diode equations and things get a lot more complex to solve using closed equations. (You might use Spice, though, for a numerical analysis.)

The above made some assumptions I should have checked. Kint (I'm glad to see) didn't make those assumptions. We can be pretty sure that \$D_3\$ is forward-biased. But what about the BE junction of \$Q_4\$? Instead of assuming about \$Q_4\$, let's not assume and instead just start from where \$R_1\$, \$D_3\$, and \$R_4\$ takes you, ignoring the rest.

In this case, you compute \$I=\frac{28\:\text{V}-700\:\text{mV}}{R_1+R_4}\approx 26.765\:\text{mA}\$. This means that \$V_D=700\:\text{mV}+R_4\cdot I\approx 27.465\:\text{V}\$. Assuming no base current at all, this would suggest about \$28\:\text{V}-27.465\:\text{V}=535\:\text{mV}\$ across the base emitter junction of \$Q_4\$.

This is way less than \$700\:\text{mV}\$. That doesn't mean it isn't forward biased, but it does mean there is very little base current flowing. Solving the equation exactly from the Shockley equation requires the LambertW function. Rather than belabor that, I get a base voltage of about \$27.467\:\text{V}\$. This means that the base emitter junction of \$Q_4\$ has about \$533\:\text{mV}\$ across it and that \$R_2\$ has only \$2\:\text{mV}\$ across it.

Even this assumes that \$700\:\text{mV}\$ is reserved for \$D_3\$. But at the indicated current in it (yet another LambertW equation to solve), it's likely higher than that.

So there's probably very close to zero base current in \$Q_4\$. Which means very little collector current, too. That's why Spice shows what it does. It's able to fully handle all of the nuances of the diode and the BJT, without making broad assumptions.

jonk
  • 77,059
  • 6
  • 73
  • 185
  • Thank you for your answer. It's easier with re-drawing the schematic. But there is something I didn't get. We find that the transistor is in saturation mode. So why Vce is not equal or close to Vcesat? – Tack Jan 14 '19 at 08:36
  • 1
    @Tack It is close to it. Did I say otherwise? Look in my text for \$200\:\text{mV}\$. – jonk Jan 14 '19 at 11:45
  • Yes, you're right. I'm sorry Is my calculation right? $$V_d = \frac{\frac{28}{R_1}+\frac{28-0.7}{R_2}+\frac{0.7}{R_4}}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_4}}$$ $$V_d = 27.437 V$$ $$I_b = \frac{V_d-V_b}{R_2} = 1.37mA $$ If the transistor is in linear mode, $$I_c = 137 mA$$ And Vce < 0, it's impossible So $$V_{ce} = V_{ce_{sat}} $$ But, I don't understande my Spice simulation, which gives Vc = 1V (and Vce = 27 V) I have similar results to verbal Kint. Vce > 1 – Tack Jan 14 '19 at 14:07
  • 1
    @Tack Yes, I'd get about \$V_D\approx 27.4377\:\text{V}\$ if I assumed exactly \$700\:\text{mV}\$ for the forward-biased junctions. So your calculation is the same as mine, or close enough anyway. All of what I wrote assumed that both PN junctions were forward-biased at 700 mV, though. I think Kint's analysis is more accurate, though, because he does NOT make that assumption. I'll write a note above to clarify. – jonk Jan 15 '19 at 03:24
  • Thanks. In your note, there is something I didn't get, how do you find 27.467V? And, I didn't understand why Vce is not less than 1V. Vce is almost equal 28V – Tack Jan 15 '19 at 15:02
  • 1
    @Tack I got it using the LambertW function (which is a closed solution to a non-linear exponential product equation.) I didn't want to belabor the development of that kind of equation (I can and I've done so here on different answers, but didn't want to repeat the effort here.) Vce is close to 28 V because, without any base current to speak of, there isn't much collector current to create a voltage drop across R3. So the collector is pulled down close to ground as a result. – jonk Jan 15 '19 at 17:40
  • Thanks, it seems that the transistor is almost close so. Where can I find the LambertW for the calculation (just the equation, I'll solve). – Tack Jan 16 '19 at 07:32
  • 1
    @tack [Click here for a fully worked process using LarmbertW](https://electronics.stackexchange.com/a/322430/38098). Separately, you can look up the function on [Wolfram LambertW](http://mathworld.wolfram.com/LambertW-Function.html). In my case above, \$R_1\$, \$R_4\$, and \$D_3\$, works out to $$V_{D_3}=V_\text{CC}- \eta\:V_T \operatorname{LambertW}{\left (\frac{I_\text{SAT}\cdot e^{\left[\frac{V_\text{CC}}{\eta\: V_T}\right]}}{\eta\: V_T} \left(R_{1} + R_{4}\right) \right )}$$\$\eta\$ is the emission coefficient and \$I_\text{SAT}\$ is the diode saturation current, in case that's not clear. – jonk Jan 16 '19 at 08:27
2

Nothing really ugly here. As suggested by Monsieur jonk, redraw your circuit including the \$V_f\$ source. Define the current \$i_1\$ flowing in \$R_1\$ then the base current \$i_b\$ and, finally, \$V_D\$ which is the voltage across \$R_4\$ with a current equal to the sum of \$i_1\$ and \$i_b\$ in series with the diode \$V_f\$. Extract, substitute these variables and solve for \$V_D\$ and voilà, you have it:

enter image description here enter image description here

A quick bias point analysis with SPICE shows the voltage at node 2 which is your \$V_D\$ not far from what the equation gives.

Verbal Kint
  • 20,420
  • 1
  • 16
  • 50
  • Thank you very much for your answer. What I found with LTspice is same as you. Do you know how to find Vc? – Tack Jan 14 '19 at 08:38
  • 1
    Happy if this could help. For \$V_c\$, you know the base current \$i_b\$, what is the collector current for a bipolar transistor? It should not be too hard to find : ) – Verbal Kint Jan 15 '19 at 06:22
  • I can find Ic if I assume the transistor. But how to prove that? Even if with it, I can't find Ic. Let's assume the transistor is linear $$I_b = \frac{V_d+V_{be}-28}{R_2}$$ $$I_b = \frac{27.4637+0,536-28}{100} = -3µA$$ $$I_c = \beta I_b =- 100 *3µ = -300µA$$ $$I_c = \frac{28-V_{ce}}{R_3}$$ $$V_{ce} = -3µ.100+28 = 27.9997V$$ $$V_{ce} = V_c_Ve$$ $$V_e+V_{ce} = V_C$$ $$V_c = 28+27.9997$$ Something is wrong....... If I assume the pnp is saturated, I have Vce = Vce_sat = 1V max Then, Vc = 27V but that's not the result with the simulation. – Tack Jan 15 '19 at 14:42