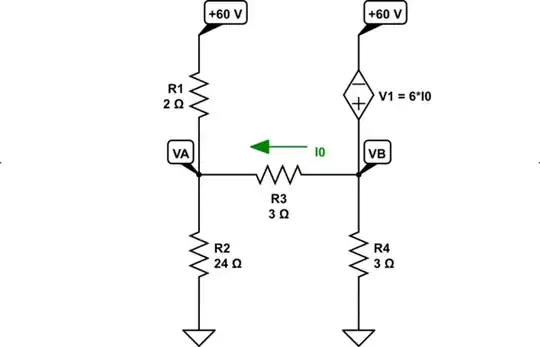
the question is to calculate v1 & iΦ, of course for nodal analysis (v1/24) + ((v1-(60+6iΦ))/3) + ((v1-va)/2) = 0, but (with va as the node left of 2 ohm resistor) how to calculate va? is it 60+6iΦ? 60-6iΦ? 60? or is it something else?
2 Answers
The first thing to do is to redraw the schematic into a somewhat better (more readable) layout. (You can read a short discussion I wrote here.)
simulate this circuit – Schematic created using CircuitLab
(Note that you get to assign exactly one node to the value \$0\:\text{V}\$. You can only do that once, to one node. No more. There are convenient places to make such assignments. But no bright line reasons to choose one over another. You can move the ground assignment to anywhere you please and the basic analysis results will be the same. The absolute values will be different. But the relative values won't change, no matter how you assign ground.)
From the above, you can easily see that:
$$\begin{align*} \frac{V_A}{R_1}+\frac{V_A}{R_2}+\frac{V_A}{R_3} &= \frac{60\:\text{V}}{R_1}+\frac{0\:\text{V}}{R_2}+\frac{V_B}{R_3}\\\\ V_B &= 60\:\text{V}+6\cdot I_0\\\\ I_0 &= \frac{V_B-V_A}{R_3} \end{align*}$$
The above is readily solvable for \$V_A\$, \$V_B\$, and \$I_0\$.
- 77,059
- 6
- 73
- 185
The left end of the 2\$\Omega\$ resistor is connected to an ideal voltage source with a given value, and the other end of that source is connected to ground. These facts determine, without further analysis, the voltage at the left end of the 2\$\Omega\$ resistor with respect to ground.
- 31,192
- 5
- 29
- 67
-
if the ground is erased, could it change nodal value? – R. Akbar Jan 09 '19 at 16:47
-
@R.Akbar You can select ***ANY*** node you want and call it "ground" or \$0\:\text{V}\$. You get to do that for exactly ***ONE*** node. Removing the ground entirely merely means that all of the voltages are relative to an unknown shared variable. That can complicate communication and make the equations look a little more complex. But no harm in it, per se. Just that it is a lot simpler to make the assignment. – jonk Jan 09 '19 at 16:58
