1

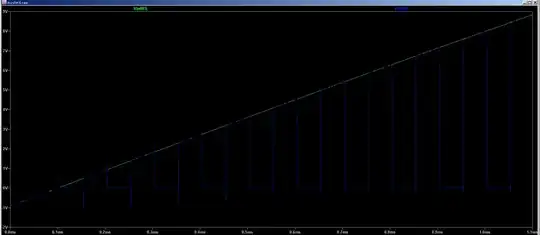
I'm looking at this mealy machine:

mealy machine

and this state table with the boolean expressions at the bottom.

state table

If you look at the \$S_1\$ boolean expression, it says \$S_1 = \overline S_1 S_0 B + S_1 A B\ \$.

Shouldn't it be \$S_1 = \overline S_1 S_0 B + S_1 \overline S_0 A B\ \$?

Why did they miss out the \$\overline S_0\$?

StainlessSteelRat
  • 7,851
  • 2
  • 18
  • 34
controlled_
  • 21
  • 4
  • What is the complete expression you think it should be? – The Photon Jan 02 '19 at 15:46
  • I didn't go through all of it.. a few though... Are you sure /S0 isn't a "don't care" i.e. does it reduce out of the final equation? Does it work for both what you wrote and what the problem stated? Just food for thought. – CapnJJ Jan 02 '19 at 16:05
  • the answers that are shown below the table i think are all correct except the answer for s'1. i think it should be s'1 = barS1 S0 B + S1 barS0 A B. why in the answers did they miss out the barS0 or am i wrong and the answers are correct? – controlled_ Jan 02 '19 at 16:13
  • yes, I understand your question... I am suggesting that you work through both what they stated and what you think it should be, and see if you get the same results. If so, then the final equation isn't dependent (i.e. "don't care") on /S0 in the 2nd term, and it is correct to not include it. – CapnJJ Jan 02 '19 at 16:36

1 Answers1

1

Actually, when you see the state representation of the FSM, you shall notice that the output is \$1\$ when both the inputs \$A\$ and \$B\$ are \$1\$ and the machine is in state \$S_2\$ which is represented by the encoding \$10\$. So, it is enough to represent the output as \begin{equation}q = S_1 AB\end{equation}. The reason that the \$ \bar{S_0}\$ is not included in the expression \begin{equation} S_1'=\bar{S_1}S_0 B+S_1 AB\end{equation} is that there is no state defined by the encoding \$11\$ and hence the state \$10\$ is actually \$1X\$ and hence it is sufficient to include just \$S_1\$.

Suzuna Minami
  • 231
  • 2
  • 9