3

I have connected the ripple counter CD4020 to an Atmega328, which sends a 50ms (low logic level) pulse to the CD4020's input each second and monitors all of its 12 outputs. However instead of incrementing the output on each pulse, the CD4020's output gets incremented on each eighth pulse.

Why is this division with the factor 8 happening? 

Pin values: 000000000000
Pin values: 000000000001
Pin values: 000000000000
Pin values: 000000000001
Pin values: 000000000000
Pin values: 000000000001
Pin values: 000000000000
Pin values: 000000000001
Pin values: 000000000010
Pin values: 000000000011
Pin values: 000000000010
Pin values: 000000000011
Pin values: 000000000010
Pin values: 000000000011
Pin values: 000000000010
Pin values: 000000000011

The datasheet also states, that the CD4020 is a 14-stage counter, but it only has 12 outputs. Why 14?

Alexander
  • 175
  • 4
  • 2
    If you look at the datasheet you linked to and see the diagram in the top-right corner on the 1st page - do you notice how the outputs are labeled? Do you see that there is no Q2 or Q3 output? – brhans Nov 27 '18 at 22:04

1 Answers1

11

We can see from the datasheet, that the CD4020 has the following block diagram:

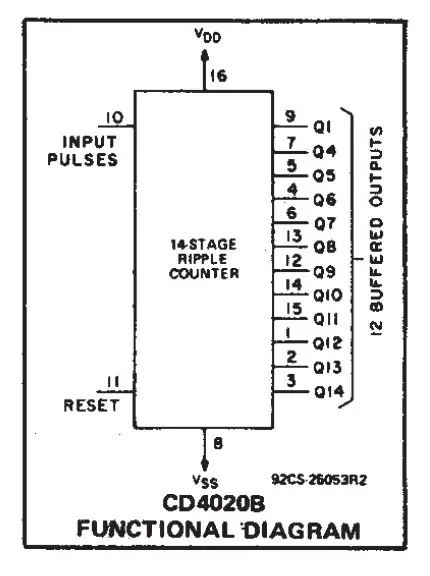
4020 Block Diagram

Notice the naming of the outputs, you have Q1, and Q4-Q14.

Note also that it is a 14-stage counter, which means the counter internally has 14 outputs.

From your data you can see that Q1 (the LSB) is toggling on every negative edge pulse as you would expect. Q1 is the first bit in the counter.

However the next available output is Q4 - this will be the fourth bit in the counter. That means that you cannot see Q2 or Q3. You would expect to see Q4 toggling at one eighth of the rate of Q1 - you are. So everything is working correctly.

Lets do a quick truth table to confirm:

  IN | Q4  Q3  Q2  Q1         Q4  Q1
 ----+----------------  ==>  --------
  \_ |  0   0   0   0          0   0
  \_ |  0   0   0   1          0   1
  \_ |  0   0   1   0          0   0
  \_ |  0   0   1   1          0   1
  \_ |  0   1   0   0          0   0
  \_ |  0   1   0   1          0   1
  \_ |  0   1   1   0          0   0
  \_ |  0   1   1   1          0   1
  \_ |  1   0   0   0          1   0
  \_ |  1   0   0   1          1   1
  \_ |  1   0   1   0          1   0
  \_ |  1   0   1   1          1   1
  \_ |  1   1   0   0          1   0
  \_ |  1   1   0   1          1   1
  \_ |  1   1   1   0          1   0
  \_ |  1   1   1   1          1   1

Yep, that matches the output you are seeing when we remove the unavailable Q2 and Q3.

The reason there are only 12 outputs is simply due to lack of pins - standard DIP packages back when the part was made were typically 8, 14, or 16 pins.

Having the higher order bits is in many applications more useful than the low order bits, so the designer chose to break them out.

Having the least significant bit is also quite useful. You can for example you feed in a pulsed analogue input (e.g from a Relaxation Oscillator). This sort of signal is no good for feeding standard digital logic, but the CD4020B uses a Schmitt trigger input to clean it up. From Q1 you will get a nice digital clock signal out, albeit at half the frequency of the oscillator.

Tom Carpenter
  • 63,168
  • 3
  • 139
  • 196
  • @Alexander Having divide by 2 can also be useful. The answer will depend on looking back in time at old circuits from the early '90's to see what they were using the part for. – Tom Carpenter Nov 27 '18 at 22:16
  • To be a little nit-picky, it's not clocked and it's negative edge sensitive. But, @Alexander, the information is otherwise completely correct :) – awjlogan Nov 27 '18 at 22:23
  • @TomCarpenter :) – awjlogan Nov 27 '18 at 22:26
  • 2
    @Alexander in fact that is then one possible use for the Q1 - it will give you a nice clock signal from a narrow pulsed input. – Tom Carpenter Nov 27 '18 at 22:26