The efficiency as ratio (to the capacitor charged energy)/(energy taken from the supply) grows as the charged voltage grows. As the charging continues the current drops, so resistive loss power drops, too. That doesn't guarantee the total dissipated energy becomes neglible when compared to the energy taken from the constant power supply, but numerical simulation shows that it happens.
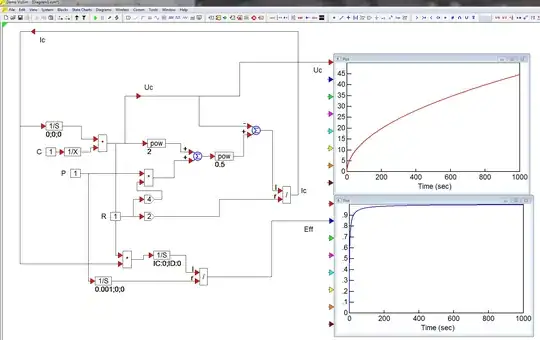
P=1W, R=1Ohm, C=1F, simulation period =1000s. The efficiency approaches 1.
The simulation principle is to present the charging current Ic as a function of charged voltage Uc, series resistance R and supplied power P. What happens can be seen by letting the charge get cumulated into an integrator like in the old analog computation days.
The charged voltage is the current integrated and divided by C. Thus we can present the input of an integrator as an expression of the output of the same integrator and parameters P, R and C.
Blocks 1/S are integrators. There are total 3 of them. One collects the charge, the other collects the supplied energy (input=P) and the third collects the charged energy (input = Uc * Ic)
Ic presented as a function of Uc, R, and P is a solution of 2nd degree equation:
R(Ic)^2 + IcUc = P ==> Ic = (-Uc + sqrt((Uc)^2+4PR)/(2R)
(sorry for typewriter look)
The used program is ancient VisSim COM. (a communication specific version). It can be considered as simplified Matlab Simulink os Scilab Xcos. I was interested in VisSim COM because it has numerous ready to use data- and radio communication math blocks such as IQ mixers, complex domain signal math, all common modulations etc...
VisSim disappeared about 4 years ago; its producer Visual Solutions was sold to a company which made premium priced much more complex packages and dropped immediately the low cost general simulator. But in July 2020 it appeared again. Windows 10 versions are unknown. I guess the last old versions are taken again to the selling list. The price is now "get a quote". I have only its demo which works with limited number of blocks and cannot save.
Simulation is as well possible in some circuit simulators. No tricky integrators are needed if a capacitor is charged with constant power source. At least Micro-Cap knows idealized math blocks There the constant power source can be built by dividing the wanted power by measured current. It works with no hiccup, no matter there should be divide by zero as the starting condition before resolving the actual first sample point. Not bad, I'd say!
The same 1000 second charging is tested in the next example. The charged voltage at node 5 is shown:
The efficiency could be calculated by collecting the energies to integrators and dividing like in the first example but as well one can calculate it (C * (Uc)^2)/(2PT) where P is the power, T is the charging period, C is the capacitance and Uc is the cumulated voltage in the capacitor.