Output resistance of MOSFET circuit

Question

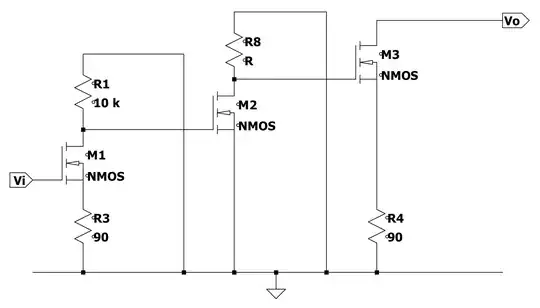
I am trying to find the output resistance \$Rout\$ of this circuit consisting of 3 n-type MOSFETs.

It is given that all 3 MOSFETs have \$g_m=4 mA/V^2\$ and output resistance \$R_o=100k\Omega\$.

^{simulate this circuit – Schematic created using CircuitLab}

The given answers to the question are to use a small-signal equivalent circuit and then just use \$Rout=R_4+R_o=100.09 k\Omega\$

The method I used was different but also uses a small-signal equivalent. My working is shown below and I get an answer of \$136.09 k\Omega\$

The equivalent MOSFET circuit has a voltage-dependent current source. I was always taught that to find the effective resistance when a dependent source is present, you can't simply add/shunt resistances together, you have to 'excite' the circuit with a voltage/current source and measure the resulting current/voltage from that source.

A quick explanation of my method: I first set input voltage to zero and 'excite' the circuit with a 1A source between VDD and the drain of the 3rd MOSFET since this is where the R_out arrow points between. The first two MOSFETs do nothing and then R_out is equal to the voltage across the 1A source divided by 1A which is just the voltage at the 3rd MOSFET drain. I then just do nodal analysis on the drain and source nodes to find the drain voltage. Note: I accidentally wrote R_out as R_o in my working.

I also simulated my circuit in PSPICE which resulted in the same drain voltage as in my answer.

Which answer is correct and if I'm wrong, where am I going wrong? Thanks for any help.

Answer 1

Probably the correct way to draw your circuit is by connecting the tops of the 10 k drain resistors together and to ground, as I assume they are in fact connected to the VDD rail, which however has no place in a small signal model and should be considered as ground. The output should be totally disconnected and rather be connected to the output terminal where the load goes, as now it is short circuited to ground (for AC). Also, g is expressed in \$ (m)A/V \$, not \$ (m)A/V^2 \$.

Big Edit:

Now I want to know exactly what is the case, and will try to calculate open output voltage and short-circuited output current in the presence of input signal \$V_i\$ and divide the two in order to get the output impedance.

So in LTSpice I drew the original circuit in a small-signal representation which is void of all things DC, and this is what it looks like:

In which \$R_8\$ should read \$R_2\$ and the '\$R\$' in the same is \$10 k \, \Omega\$.
If the mosfets in this circuit are replaced by a simple equivalent circuit with only \$g\$ and \$R_o\$, then we get the circuit below:

and in this representation we can replace the current sources and internal resistances with voltage sources as in the picture below:

Going from left to right through the circuit we can clearly see that the current through \$R_3\$ is $$I_{R_3} = g R_o U_{gs_1} / (R_1 + R_3 + R_5) $$

Further, $$U_{gs_1} = U_{g_1} - R_3 I_{R_3} $$ so that $$ I_{R_3} = g R_o (V_i - R_3 I_{R_3})/(R_1 + R_3 + R_5) $$. Rearranging this gives $$ g R_o V_i / (R_1 + R_3 + R_5) = I_{R_3} \{R_1 + (1 + g R_o)R_3 + R_5\}/(R_1 + R_3 + R_5) $$ from which we find $$ I_{R_3} = g R_o V_i / \{R_1 + (1 + g R_o)R_3 + R_5\} $$

Now, for the second mosfet. It's gate voltage we find from $$ U_{g_2}=-R_1I_{R_3} = -gR_oR_1V_i/\{R_1+(1+gR_o)R_3+R_5\}$$ and we find the current through \$R_6\$ $$ I_{R_6}=-(gR_o)^2R_1V_i/\{R_1+(1+gR_o)R_3+R_5\} $$

Now up to the third mosfet we can write its gate voltage $$ U_{g_3} = -R_2I_{R_6} = (gR_o)^2R_1R_2V_i/\{R_1+(1+gR_o)R_3+R_5\} $$ Now we also have $$ U_{gs_3} = U_{g_3} - R_4I_{R_4} $$ and finally we can now calculate both open output voltage and short circuit output current. Namely if the output is open, \$I_{R_4}=0\$ and \$U_{gs_3}=U_{g_3}\$ and we can write the open output voltage as $$ U_{out_{open}} = -(gR_o)^3R_1R_2V_i/\{R_1+(1+gR_o)R_3+R_5\} $$ and if the output is short circuited then \$U_{out}=0\$ and we can write $$ I_{out} = -I_{R_4} = -g(U_{g_3}-R_4I_{R_4}) = -gU_{g_3}/(1+gR_4) $$ which, rearranged, gives us the short circuit output current $$ I_{out_{short}} = -(gR_o)^3R_1R_2V_i/\left[\{R_1+(1+gR_o)R_3+R_5\}R_o(1+gR_4)\right] $$ the form of which looks eerily similar to that of \$U_{out_{open}}\$ and the quotient of the two becomes simply $$ Z_{out} = \frac{U_{out_{open}}}{I_{out_{short}}} = (1+gR_4)R_o $$ With \$g = 4mA/V\$ and \$R_o=100\, k\Omega\$, this becomes $$ Z_{out} = (1+4.10^{-3}.90).10^5 = 136 \, k\Omega $$

Answer 2

Due to the negative feedback at the source, the output impedance will be always higher than the sum of RDS and the RS, where the latter is the resistance at the source. In this case, the loop gain is relatively small (gm*R4=0.36), that's why the modest increase in comparison to a bare MOSFET.