Finding the Transfer Function of Spring Mass Damper System

Question

I have been going through Ogata Modern Control Engineering book and working through several exercises to improve my understanding of basic control principles. I came across the following example which I am struggling to solve.

I need to come up with the transfer function that models this vibration jig. The questions are as follows:

In this example you will be analysing a vibration test rig (Fig. 1). This system consists of a table of mass M, and a coil whose mass is m. A permanent magnet rigidly attached to the ground provides a steady magnetic field. The motion of the coil, , through the magnetic field induces a voltage in the coil that is proportional to its velocity, ̇, as in Eq. 1. = ̇ [eq.1]

The passage of current through the coil causes it to experience a magnetic force proportional to the current as in Eq. 2. = [eq.2]

Question: Obtain a parametric transfer function with output to input .

Some questions I am finding hard to answer but affect the whole T.F are:

• If K2 and B2 are compressed by a distance Z, (when moving upwards
  due to the coil interacting with the magnetic field) does this mean that k1 and b1 are extended by the same distance Z?

• If m (coil) moves upward by 2cm, does M (table) also move upwards by 2cm?

---

What I need to do:

• Come up with two separate free body diagrams, one for the mass M of the table and one for the mass m of the coil.
• Sketch one circuit diagram including back emf.
• Transform to s-domain.
• Solve simultaneously.

What I have done so far:

• Draw to separate free body diagrams and extract equations.

• Draw the circuit diagram and extract equation.

• Convert to s-domain.

Using MATLAB function solve I managed to get 2 different 5th order transfer functions (one for each method I propose below), however, I am not sure which one is correct, and why.

---

Overall System :

This is a diagrammatic representation of how I think the vibration test jig can be modelled, excluding the electrical part.

---

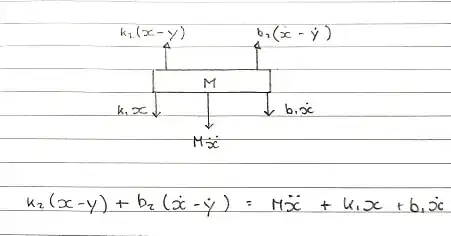
Free Body Diagram 1 - Table - Upward Convention

Springs k1 and k2 and dampers b1 and b2 are modeled separately. Since they cannot be added together and viewed as one, their compression and extension are separate.

The upward force is coming from k2 and b2 which are attached to the coil. These are experiencing an upward motion.

Equation in the s-domain :

Ms^2X + b1sX + k1X = b2s(X-Y) + k2(X-Y)

---

Free Body Diagram 2 - Coil - Upward Convention

The coil is experiencing a force upwards, however the spring and damper are holding it back, thus acting in the opposite direction.

Equation in the s-domain :

Fem = Ms^2Y + b2s(X-Y) + k2(X-Y)

---

The two different methods are shown above for the FBD of the table lead to different equations in the s-domain and different transfer functions.

What is the correct Free Body Diagram for the table and coil?

Answer 1

Intro

M and m have only one degree of freedom; both can move vertically only. The magnetic force directly acts upon the magnet m, not on the mass M.

To demystify the picture a bit it could be helpful to think of the magnet as positioned on the other side of the table. The picture has been drawn in LTSPICE, and that has no arrows. So the closest approximation to an arrow is the output pin, and as those can only point horizontally to the right, the whole picture is rotated \$90^o\$ to the right. For the same reason the arrows '-y' and '-F' point to the right whereas I would have liked to have drawn arrows 'y' and 'F' to the left. Further, the right \$b_1\$ should read \$b_2\$.

Now it is clear that this is a series connection of masses with dynamical elements between them, so we start writing down the motional equations from the right to left, starting with the electrical equation for m first, which will contain V, y and F.
After that we will write the motional equation for m and for M.
As M isn't affected by a magnetic force, this last equation will give us y as a function of x, which will be used in the first equation to relate x to V.

Electrical

The magnetic force and the movement of the magnet are coupled via the voltage across the coil. And because $$e=\alpha \dot y \, , \, F=\beta i \, , \, V- e=Ri+L \dot i $$ and assuming L is independent of y, we have $$V-e = V - \alpha \dot y = R i + L \dot i = \frac{R}{\beta}F+\frac{L}{\beta}\dot F $$

Now we have \$ y\$ in terms of \$F\$ (and \$V\$), and we can write the equations of motion by adding all forces upon the moving objects and forcing them to be zero (by law).

The magnet

$$ F+m \ddot y + b_2 \left(\dot y - \dot x \right) +k_2 \left(y-x \right) =0 $$ We can solve the relationship above between F and y in the s-domain $$ V-\alpha \dot y = V(s)-\alpha s y = \left(R+Ls\right) i = \left(R+Ls\right)F/\beta $$ and therefore $$ F=\frac{\beta}{R+Ls}\left(V(s)-\alpha s y\right) $$ The sum of the forces on the magnet is zero, so (and for readability the positions are not yet transformed to the s-domain) $$\frac{\beta V(s)}{R+Ls}-\frac{\alpha \beta }{R+Ls}sy+m\ddot y +k_2\left(y-x\right) + b_2\left(\dot y-\dot x\right)=0 $$ After transforming to the s-domain this equation looks like $$ \frac{\beta V(s)}{R+Ls}-\frac{\alpha \beta }{R+Ls}sy+ms^2 y +k_2\left(y-x\right) + b_2s\left( y- x\right)= 0 $$ After re-grouping this becomes $$ ms^2y+\left(b_2-\frac{\alpha \beta }{R+Ls}\right)sy +k_2y -b_2sx - k_2x =-\frac{\beta V(s)}{R+Ls} $$ Isolating \$x\$ and \$y\$ we get $$ \left(ms^2+b_2s-\frac{\alpha \beta s}{R+Ls}+k_2\right)y-\left(b_2s+k_2\right)x = -\frac{\beta V(s)}{R+Ls} $$

The moving table

For the moving table the governing equation is $$ M\ddot x +k_1x+b_1\dot x +k_2\left(x-y\right)+b_2\left(\dot x-\dot y\right)=0 $$ After transforming to the s-domain this equations looks like $$ Ms^2 x +k_1x+b_1s x +k_2\left(x-y\right)+b_2s\left( x- y\right)=0 $$ After re-grouping this becomes $$ -b_2sy -k_2y +Ms^2x +\left(b_1+b_2\right)sx +\left(k_1+k_2\right)x =0 $$ Isolating \$x\$ and \$y\$ we get $$ - \left( b_2s+k_2 \right) y + \lbrace Ms^2 + \left( b_1+b_2 \right)s +k_1+k_2 \rbrace x = 0 $$ Rewrite this equation to get y in terms of x. $$ y = \frac{Ms^2 + \left( b_1+b_2 \right)s +k_1+k_2}{b_2s+k_2}x $$

Ensemble

Put \$y=f(x)\$ from above into the relationship between \$x\$, \$y\$ and \$V\$ for the magnet: $$ \left[ \left(ms^2+b_2s-\frac{\alpha \beta s}{R+Ls}+k_2\right) \frac{Ms^2 + \left( b_1+b_2 \right)s +k_1+k_2}{b_2s+k_2} - \left( b_2s+k_2 \right) \right] x = -\frac{\beta V(s)}{R+Ls} $$

If we multiply both sides of the equation with \$R+Ls\$ we get

$$ \left[ \lbrace (R+Ls) \left( ms^2+bs+k_2 \right) - \alpha\beta s \rbrace \frac{Ms^2+(b_1+b_2)s+(k_1+k_2)}{b_2s+k_2}-(R+Ls)(b_2s+k_2)\right]x = -\beta V(s) $$

Next we multiply both sides with \$b_2s+k_2\$ and get

$$ \left[ \lbrace (R+Ls) \left( ms^2+bs+k_2 \right) - \alpha\beta s \rbrace \lbrace Ms^2+(b_1+b_2)s+(k_1+k_2)\rbrace - (R+Ls)(b_2s+k_2)^2 \right]x = - (b_2s+k_2) \beta V(s) $$

From visual inspection it follows that we can expect a transfer function \$ x(s)/V(s) \$ with a maximum order of 1 in the nominator and of 5 in the denominator. It is possible that one zero cancels out with the one pole, but that is speculative and would require some more rewriting to find out.