In the treatment of metamaterials, optical problems and antennas, very often a simplified model is extracted by considering only lumped elements. In some cases this is fairly obvious, for example in this paper, which shows a split-ring resonator with its equivalent circuit.
The straight wires act like inductors, and the capacitor-shaped element in the middle acts like a .. capacitor. So far so good.
But how would this model change if I include a dielectric slab and a ground plane behind the element?
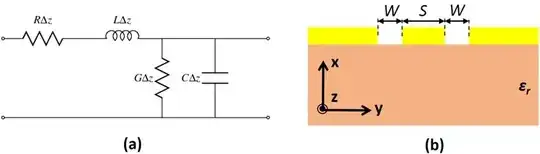
Or how can I approach this in other cases, for example for this coplanar waveguide?
Is there a cookbook-style, systematic recipe how to set up the equivalent circuit of such a system? Where do I start? It seems to me there are loads of capacitances and inductances everywhere - when should I stop including them? And where do the geometric and electric parameters of the original structure come in when evaluating the final circuit (surely I would like to calculate the inductance from the crosssection and length of the wire)?
An answer would be either an explanation how it works in general, insightful examples of different cases or some guidelines as to where I can read about it in detail. At the moment, these equivalent circuits seem to fall out of the sky for me and it's not clear to me, how authors arrive at them.