Why is 50 Ω often chosen as the input impedance of antennas, whereas the free space impedance is 377 Ω?

Question

In order to efficiently deliver power to a different part of a circuit without reflection, the impedances of all circuit elements need to be matched. Free space can be regarded as a further element, since a transmitting antenna eventually should radiate all power from the transmission line into it.

Now, if the impedances in the transmission line and in the antenna are matched at 50 Ω, but the impedance of free space is 377 Ω, won't there be a impedance mismatch and consequently a less-than-optimal radiation from the antenna?

As far as I gathered from literature and discussions online, the antenna acts as an impedance transformer between the feed line and free space. The argument goes: no power from the feed line is reflected and must go to the antenna. The antenna can be assumed to be resonant and therefore radiates all its power into free space (disregarding heat losses, etc.). This means that there is no reflected power between antenna and free space, and the transition between antenna and free space is therefore matched.

The same should be true in the reverse direction for a receiving antenna (Reciprocity Principle): a wave in free space (\$Z_0\$) impinges onto an antenna, and the received power is fed into the transmission line (again through impedance transformation). At least in one paper (Devi et al., Design of a wideband 377 Ω E-shaped patch antenna for RF energy harvesting, Microwave and Optical Letters (2012) Vol. 54, No. 3, 10.1002/mop.26607) it was mentioned that a 377 Ω antenna with a separate circuit to match it to 50 Ω was used to "achieve a wide impedance bandwidth" with a high power level. If the antenna normally is already the impedance transformer, what is the matching circuit needed for then? Or alternatively, under what circumstances is the antenna not also the impedance transformer?

Some helpful sources and discussions I found:

• Klaus Kark, Antenne und Strahlungsfelder (in German)
• Impedance Matching (http://www.phys.ufl.edu/~majewski/nqr/reference2015/nqr_detection_educational/Impedance_matching_networks.pdf)
• Forum discussion that mentions impedance transformation for an inverted-F antenna (http://www.antenna-theory.com/phpbb2/viewtopic.php?t=776&sid=dede0d4127170d16cc3a583ab0929f3e)
• Some general notes about antennas (http://fab.cba.mit.edu/classes/862.16/notes/antennas.pdf)

Answer 1

The input impedance of certain devices/circuits (transformers) does not neccessarily need to match their output impedance.

Consider a 50Ω (or whatever impedance) antenna as transformer that transforms 50Ω (wire side) to 377Ω (space side).

The impedance of the antenna is not (only) given by the impedance of free space but (also) by the way it is constructed.

So the antenna does match the impedance of free space (on one side); and ideally also the impedance of the circuit (on the other side).
Since the space side's impedance is always the same (for all kinds of antennas operated in vacuum or air), it doesn't need to be mentioned.
Only the wire side is what you need and can care about.

The reason 50Ω or 75Ω or 300Ω or ... is choosen as antenna impedances is because of practical reasons to construct particular antennas/transmission lines/amplifiers with that impedance.

A possible ansatz for calculating the radiation resistance \$R\$ of an antenna is:

Find an answer to the question: "How much power \$P\$ (average over one period) is radiated if a sinusoidal signal of given voltage (or current) amplitude \$V_0\$ (or \$I_0\$) is applied to the antenna?"

Then you get \$R = \frac{V_0^2}{2P}\$ (or \$=\frac{2P}{I_0^2}\$)

You get radiated power \$P\$ by integrating the Poynting vector \$\mathbf{S}\$ (=radiated power per area) over the sphere enclosing the antenna.

The Poynting vector is \$\mathbf{S} = \frac{1}{\mu_0} \mathbf{E} \times \mathbf{B}\$ where \$\mathbf{E}\$ and \$\mathbf{B}\$ are electric/magnetic fields caused by the voltages and currents in your antenna.

You can find an example for such a calculation in the Wikipedia acticle about "Dipole antenna", in paragraph Short Dipole.

Answer 2

All the answers name some valid points, but they fail to really answer the question which I want to repeat for clarity:

Why is 50 Ω often chosen as the input impedance of antennas, whereas the free space impedance is 377 Ω?

The Short & Simple Answer

These two impedances have no relation at all. They describe different physical phenomena: the antenna input impedance is not related to the 377 Ω free-space impedance. It is only by accident that the unit of both terms is the same (i,e., Ohms). Furthermore, 50 Ω is just a common value for characteristic impedances of transmission lines etc., see the other answers.

Basically, the input impedance of an antenna, any other resistance or reactance, and characteristic impedances are circuit-level descriptions for handling voltages and currents, while the free space wave impedance is for describing electric and magnetic fields. In particular, the (real-valued) 50 Ω input impedance means if you apply 50 V of voltage at the antenna feed, 1 A current will flow trough the antenna feed point. The free-space impedance has no relation to any antenna or material configuration. It describes the ratio of electric and magnetic fields in a propagating plane wave, which is approximatly obtained in an infinite distance to a radiating antenna.

The Longer Answer

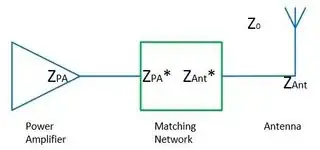
The first impedance mentioned in the question is the input impedance of the antenna, which is a sum of radiation resistance, loss resistance and reactive components which are described as the imaginary part. It is related to currents \$I\$ and voltages \$V\$ at the feeding pont on a circuit-description level, i.e., $$R = \frac{V}{I}\,.$$ Changing the feeding point of the antenna, the value of this radiation resistance might change (this fact is employed e.g. for the matching of inset fed microstrip patch antennas). The radiated fields, however, stay basically the same.

This impedance \$R\$ of the radiation resistance is the same kind as of a resistor or the transmission line characteristic impedance of coaxial lines or microstrip lines, since these are also defined via voltages and currents.

The radiation resistance is not a real resistance, it is just a model for the radiation case (i.e., operating the antenna to transmit power), where power gets lost from the circuit point of view since it is radiated away. (On a related note: using this resistance for the receive case is misleading, since there occurs no loss in the radation resistance. It is still important for matching, though.)

The second impedance is a wave impedance of the fields, which describes the ratios of electric (\$E\$) and magnetic (\$H\$) fields. The free-space impedance, for instance is given as $$ Z_{0,\mathrm{free\,space}} = \frac{E}{H} = \pi 119,9169832\,\Omega\approx377\,\Omega\,.$$ (This exact value was used before 2019, see Wikipedia on the free-space impedance) We can immediately see that fields and voltages have a relation that might change with geometry etc, or there might be no unique definition of voltages (e.g., in a hollow waveguide).

To make this lack of relation of these kinds of impedances more clear, an example might help. In the very simple case of the TEM wave inside of a coaxial cable, we know how to calculate the characteristic impedance the coaxial cable based on the geometry as $$Z_{0,\mathrm{coax}}=\frac{1}{2\pi}\sqrt{\frac{\mu_0}{\epsilon_0}}\ln\frac{r_{\mathrm{outer}}}{r_{\mathrm{inner}}}\,,$$ if we assume that the filling material is vacuum. This is a characteristic impedance (of the transmission line) for the currents and voltages of this line, and this is the kind of impedance which should be matched to the input impedance of an antenna.

However, having a look at the fields inside the cable, we find that the electric field has only the radial component (exact values are irrelevant in this context) $$E_r \propto \frac{1}{r \ln(r_{\mathrm{inner}}/r_{\mathrm{outer}})} \,.$$ More interestingly, the \$B\$ field has only a \$\phi\$-component which is a scaled version of the electric radial field $$B_\phi = \frac{k}{\omega}E_r=\frac{1}{c}E_r\,,$$ where \$c\$ is the speed of light, which is from free space (!) because the medium inside is free space. By using $$ B = \mu H\,,$$ we finally know the phi-component of the magnetic field as $$H_\phi =\frac{\sqrt{\epsilon}}{\sqrt{\mu}}E_r=Z_{0,\mathrm{free\,space}}E_r\,,$$ Therefore, the ratio of electric and magnetic fields is constant and only medium dependent; however, it does not depend on the geometry of the cable.

For free space inside the coaxial cable, the wave impedance is always approximately 377 Ω, while the characteristic impedance is geometry-dependent and can take any possible value from almost zero to extremely large values.

Conclusion & Final Remarks

If we look again at the example of the coaxial cable and leave it open at the end, achieving a characteristic impedance of ~377 Ω does not relate to anything about the fields. Any coaxial cable filled with air has a wave impedance of ~377 Ω, but this does not at all help to make the open piece of coaxial cable a good antenna. Therefore, a good definition of antenna does not relate at all to impedances, but reads

An antenna is a transducer from a guided wave to an unguided wave.

Answer 3

50 ohms is a convention. It's much more convenient if a room full of equipment all uses the same impedance.

Why is it the convention? Because coax is popular, and because 50 ohms is a good value for coax impedance, and it's a nice round number.

Why is it a good value for coax? The impedance of coax is a function of the ratio of the diameters of the shield and center conductor, and the dielectric material used:

$$ Z_0 = {138 \over \sqrt{\epsilon}} \log_{10}\left(D\over d\right) $$

Or rearranged algebraically:

$$ {D \over d} = 10^{\sqrt{\epsilon} Z_0 / 138} $$

where:

• \$Z_0\$ is the characteristic impedance of the coax
• \$\epsilon\$ is the dielectric constant (air is 1, PTFE is 2.1)
• \$D\$ is the diameter of the inside surface of the shield
• \$d\$ is the diameter of the outside surface of the center conductor

As the characteristic impedance increases, the center conductor must become smaller if the shield geometry and dielectric material remain constant. For \$Z_0 = 377\:\Omega \$, and PFTE dielectric:

$$ {D \over d} = 10^{\sqrt{2.1}\ 377 / 138} = 9097 $$

So for a coax cable with an outside diameter of 10 mm (RG-8, LMR-400, etc are approximately this size), the center conductor would have to be 10 mm / 9097 = 1.10 micrometers. That's impossibly fine: if it could even be manufactured with copper it would be extremely fragile. Additionally loss would be very high due to the high resistance.

On the other hand, the same calculation with \$Z_0 = 50\:\Omega \$ yields an inner conductor of approximately 3 mm, or 9 gauge wire. Easily manufactured, mechanically robust, and with sufficient surface area to result in acceptably low loss.

OK, so 50 ohms is a convention because it works for coax. But what about free space, which we can't change? Is that a problem?

Not really. Antennas are impedance transformers. A resonant wire dipole is a very easy to construct antenna, and it has a feedpoint impedance of 70 ohms, not 377.

It's not such a foreign concept. Air and other materials also have an acoustic impedance, which is the ratio of pressure to volume flow. It's analogous to electrical impedance which is the ratio of voltage to current. Somewhere in your house you probably have a speaker (perhaps a subwoofer) with a horn on it: that horn is there to take the very low acoustic impedance of air and transform it to something higher to better match the driver.

An antenna serves the same function, but for electric waves. The free space into which the antenna radiates has a fixed 377 ohm impedance, but the impedance at the other end depends on the geometry of the antenna. Previously mentioned, a resonant dipole has an impedance of 70 ohms. But bending that dipole so it forms a "V" instead of a straight line will decrease that impedance. A monopole antenna has half the impedance of the antenna: 35 ohms. A folded dipole has four times the impedance of the simple dipole: 280 ohms.

More complex antenna geometries can result in any feedpoint impedance you like, so while it would be technically possible to design an antenna with a feedpoint impedance of 377 ohms, but you wouldn't want to use it with coax for the reasons above. But perhaps twin-lead would work, though there wouldn't be any particular advantage to 377 ohm twin-lead.

At the end of the day, the antenna's job by definition is to convert a wave in one medium (free space) into a wave in another medium (a feedline). The two don't usually have the same characteristic impedance and so an antenna must be an impedance transformer to do the job efficiently. Most antennas transform to 50 ohms because most people want to use 50 ohm coax feedlines.

Answer 4

This question is a good example of over interpreting electrical engineering rules that were devised to make the physics more manageable in practical contexts. Impedance simply isn't that important.

The energy of a radio wave is embodied in the electric and magnetic fields distributed in a spatial volume. Maxwell's equations establish requirements for the relationships among those fields, and the homogenous equations imply that a disturbance from equilibrium will propagate. The latter is evident from the fact that the wave equation is easily derived from the fundamental equations.

In the wave equation there is an implied velocity of propagation that is the reciprocal of the square root of the product of the magnetic permeability and electric permittivity of the medium of propagation.

The square root of the quotient of those two quantities has units of impedance, and when the medium in question is a vacuum or air, it is called the 'radiation impedance of free space'.

This phrase refers to the ease (or difficulty) of establishing a non-equilibrium electro-magnetic disturbance. Loosely, it is a measure of the capacity of a volume of the medium to store energy in electro-magnetic form. More energy requires more volume or you risk non-linear breakdown. Very loosely, we are quantifying how hard it is to push energy into the system.

In a transmission line, say an old fashioned twin lead, we have a similar situation with different boundary conditions. The energy in the line is stored (transiently) in the oscillating electric field between conductors and the oscillating magnetic field about the conductors. This energy can propagate in two directions. If you have equal amounts of energy propagating in both directions, you have resonance or a standing wave. If you have matched terminations, energy leaves the line when it gets to the end and does not reflect or propagate back. It is important to understand that the power is transmitted in the insulator, not the conductors. The conductors are present only to provide boundary conditions, and the charge carriers in the conductors oscillate essentially in place, providing terminals for electric fields, and coupling the electric and magnetic fields. These ideas apply equally well to coaxial lines, but it is easier to visualize in a twin lead.

Like free space, a transmission line has a characteristic impedance that is a measure of its capacity to temporarily store energy distributed along its length. This impedance is dependent upon the geometry of the conductors (boundary conditions) and the relative permeability and permittivity of the materials from which the line is fabricated. Likewise, there is a characteristic propagation velocity that is typically a substantial fraction of the velocity of light in a vacuum.

The requirement for 'matching' impedances arises from the physics of wave reflection. Obviously any reflected energy is not propagated out of the system. A match eliminates reflected energy. It is important to realize that broadband matches are difficult. Matches are typically tuned to the specific design frequency of the system, and out of band signals may exhibit significant reflections.

In a resonant feed line, this fact is exploited by driving the line at its resonant frequency. At resonance, the line impedance is purely resistive. The difficulty is, you need to control the feed line length precisely, and it is only useful at its resonant frequency.

A more practical compromise is to match impedance. Then the feed line may be any reasonable length, and the signal may be a composition of many frequencies, or many independent signals, within the limitations of the bandwidth of the match.

A simple antenna like a dipole is operated at resonance. It is a resonant feedline. It therefore presents a purely resistive characteristic impedance (dependent on geometry and physics) at its design frequency. A line matched to that impedance will deliver all of its energy to the antenna. The antenna, being a resonant feedline, in turn delivers all of its energy to the next system, which is typically free space. It does this because at its design frequency, there is no reactive impedance. If you need to push more energy, you need to drive the antenna harder, which raises the peak voltages and currents in the antenna, which increases the amount of energy pushed out into free space during a given cycle. Obviously there are limitations imposed by non-linear breakdown.

A broadband antenna is really just a lossy feedline. Within its design bandwidth, all energy is radiated by the time an oscillation reaches the end of the feedline. Such antennas typically embody conical geometry in some form, with the low frequency limit set by the base of the cone and the high frequency limit set by practal limits on the pointiness of the cone.

Answer 5

I'm doing my first steps in antenna and RF field. I was learning about Antenna Impedance when I found this question and I will try to answer it. Hopefully I have understood the question! Sorry if the answer looks stupid, I'm just a "BEGINNER" :)

You said "Why is 50 Ω often chosen as the input impedance of antennas, whereas the free space impedance is 377 Ω?", I think the answer is already included in the question. Yes, it's the word "INPUT". The 50 Ohm is chosen as an input not as an output impedance, if we want to transmit or receive the maximum power between the coaxial line and the antenna we have to match their impedance.(in this case is 50 Ohm because of the standards) If you chose 377 Ohm as the input impedance of the antenna to match it to the air impedance you will lose the power transmission between the coaxial line and the antenna.
If we consider the antenna as an element of the circuit that has an input and an "output impedance" it will look as follows:

^{simulate this circuit – Schematic created using CircuitLab}

Answer 6

The radiation resistance, \$\small R_r\$, of a half-wave dipole is \$\small 73\Omega\$. This relates directly to the feedpoint impedance, i.e. this is the impedance presented to the transmission line by the antenna at the design frequency.

\$\small R_r\$ is related to the impedance of free space (i.e. the impedance seen by an E-M wave travelling in free-space), but is not equal to it.

Answer 7

"...In order to efficiently deliver power to a different part of a circuit without reflection, the impedances of all circuit elements need to be matched...."

This is your assumption. And it is correct, but not in the case of antennas.

Because in antennas, we have "reflection". Power applied to the feed point (in a dipole, for example) travels down to the end of the wire, and is reflected back to the feed point, where (if resonant) it will meet a voltage or current 180 degrees out of phase, thus canceling, and represented by the (so-called) standing wave.

So, the applied power bounces back and forth in the antenna wire until all is radiated or lost as heat. So it does not matter if the antenna impedance is different than free space. What really matters, practically speaking, if the energy is reflected back into the transmitter and warms the final amp device, thus wasting the power/energy appliled. This happens when the impedance of the final amp does not match the antenna system (transmission line plus antenna). But once the antenna system is matched to the transmitter, almost all the energy will be transmitted to free space (except for resistance in the wire, which is usually negligible. Or so I am told.

And to comment on the answer by Laurin Cavender WB4IVG: In theory, there is no difference between theory and practice.

Answer 8

All this is good in theory but what works in practice is a different story. I have been a communications engineer for the better part of 50 years. What we have to keep in mind here is we are attempting to explain a device called an antenna and why it does or does not work, or how well it does or does not do its job. Yes a new student can usually make a functional device from all these calculations, however that is not always true. I have built some very exacting antennas from theory that simply performed very poorly if at all. A good example is the J pole the performance is often not at all what one would expect even if when hooked up to very fancy antenna test equipment i.e. VNA's, it looks like it should be a great radiator and receptor when in fact it was more of a dummy load. Practice and theory often don't intersect. 50 ohms has been mentioned, yes it is a great compromise between the worlds of 37.5 and 73 ohms and it works well for that, in fact 50 was chosen because it worked in practice and it was easy to build from existing materials. In particular 1/2 inch water pipe inserting insulators and a center conductor for use on US Navy ships for WWII. Isolation had to be had for the feedlines to go from the antennas on deck to the equipment located within the safety of the ship. Before WWII there were literally Shacks "Radio Shacks" and I don't mean the defunct electronics stores, built right out on the main deck so as to be able to conduct the antennas to the radios. Even in the newer (at the time) ships the radio room was built on the main deck on an outside wall. Now for obvious safety reasons in a war ship the radio room should never be on deck or easily exposed to enemy fire, equipment and personal safety was a must so coax was born. Yes there were theoretical applications before that but not in general practice, there was shielded wire in use but it was not coaxial nor did it need to be, but to conduct signals from above deck to below deck and vice versa a different feedline than twinlead or ladder line was needed, both to protect the signals coming and going but also to protect the personnel and other things like gunpowder from the RF. Antennas are much the same. I often see mention of 1/4 wave antennas mentioned, truth is there really is no such thing. Nearly all practical antennas are some sort of 1/2 wave dipole. In the case of the 1/4 wave the other half of the antennas is usually the car or some other ground plane. As for 377 ohms to 50 or any other impedance it is all about feed point and or literal angle of the antenna, such as the "V" antenna mentioned earlier. Take for example a 1/2 wave end fed antenna it needs somewhere between a 9:1 to a 12:1 Balun Transformer to make it match and work. As does the Off Center Fed Dipole. Now there is that magical and sometimes nasty word BalUn! It is very simply nothing bad or magical it is simply a matching transformer. Often used to go from a balanced feedline or antenna to a unbalanced feedline or antenna! Does the transformer know balanced from unbalanced, NO it does not. In fact it does not even know what the impedance is, it only knows ratios i.e. 1 to 1, 4 to 1 or 9 to 1. Again I point out practice is not THEORY, thousands upon thousands of 4:1 Baluns are in use all over the world matching 50 ohm devices (Radios) and feedlines usually coax to 300 400 and even 600 ohm antennas. Do they work, fantastically they do, are they text book correct, not on your life, but then again all this would be moot if it did not work in practice! So quit worrying about the numbers being correct they are at best guidelines, what works, WORKS! Besides 377 ohms is theoretical freespace and just like isotropic Virginia It Simply Does Not Exist!