Input impedance of a one stage voltage amplifier?

Question

This is not a school/university assignment; I'm a physicist trying to learn some electronics. I'd like to calculate the input impedance of the following circuit.

^{simulate this circuit – Schematic created using CircuitLab}

We know that C1 has a reactance of \$X_{C1}=\frac{1}{2\pi f C1}\$, which must be taken into account. That's roughly all that I know! For example I don't know if R2, C2 and the impedance of the output device are important in the calculation of input impedance as well. Also, I'd like to know the equations which show that the input impedance increases by replacing Q with a Darlington pair.

Answer 1

For typical sensible design values, the input impedance is dominated by the transistor base, with some effect from the bias resistor(s). The coupling capacitor is typically chosen to have negligible impedance at the frequencies of interest, so you can usually ignore that.

If you use the hybrid-\$\pi\$ model for the transistor, the transconductance of the transistor gm is Ic/Vt or about Ic * 40 at room temperature.

Vt= kT/q where k is the familiar Boltzman constant, T is the temperature (Kelvin) and q is the charge on an electron. It's about 25mV at room temperature.

The value of r\$\pi\$ is \$\beta_0\$/gm, where beta is the current gain of the transistor at the operating point (it's a parameter of the transistor and can vary over a wide range for a given part number, often more than 2:1).

You should also take the effect of the bias resistor R2 into account, however it's not as simple as the resistor in parallel because it's affected by the dependent current sink in the transistor, so it's effectively reduced by the voltage gain of the amplifier. More detailed information in general here. Loading the amplifier output will reduce the voltage gain so the effect due to the bias resistor will be less. If you split the bias resistor into two and bypass it to ground you can get a more constant input impedance- just the r\$\pi\$ in parallel with the left part of R2 (with Xc1 in series, but usually that's negligible).

So to pick some reasonable values, if the collector current (a design parameter) is chosen to be 1.0mA, and beta is 300, then gm = 0.04A/V and the input resistance due to the base is 300/0.04 = 7.5K\$\Omega\$.

Higher beta (as a darlington would have) proportionally increases the input resistance due to the base. You can also increase the bias resistor value.

Answer 2

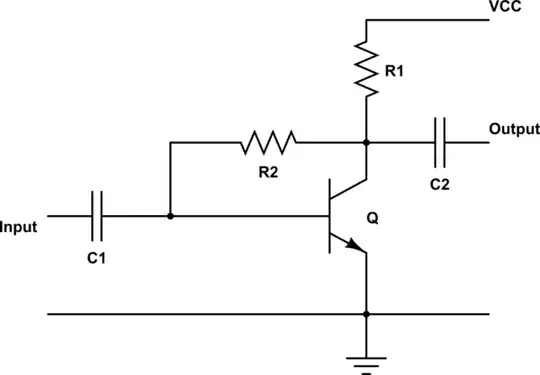
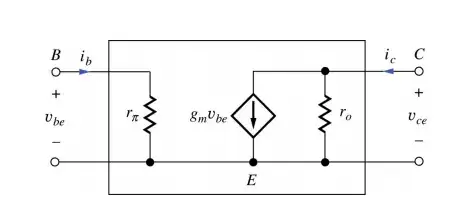
Due to the fact that the bipolar transistor is a highly nonlinear device to simplified the circuit analysis we are using the highly linearized BJT's small-signal model. True only for "small" AC signal only (10mV peak).

http://www.ittc.ku.edu/~jstiles/412/handouts/5.6%20Small%20Signal%20Operation%20and%20Models/section%205_6%20%20Small%20Signal%20Operation%20and%20Models%20lecture.pdf

If we replace the transistor in your circuit with the hybrid-π model, your circuit will look like this:

^{simulate this circuit – Schematic created using CircuitLab}

Where:

\$r_{\pi} = \frac{\beta}{g_m}\$

\$g_m = \frac{I_C}{V_T} \approx \frac{I_C}{26mV}\$

\$I_C\$ - is a quiescent collector current (DC collector current).

In the hybrid-π model, we are treating the BJT as a voltage controlled (vbe) current source (Ic). That means that the collector current Ic is determined and controlled by the Vbe voltage, and not by the input current base Ib.

And if you plot \$I_C\$ vs \$V_{BE}\$

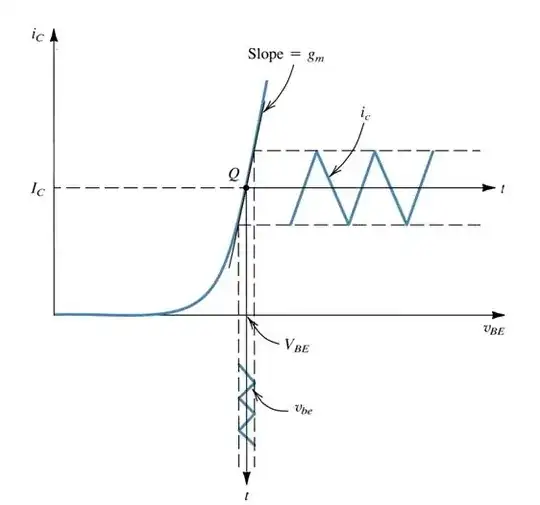
The \$g_m\$ is the slope of this curve

In general transconductance \$g_m\$ in simple term is a "gain" for any transconductance amplifier. And because transconductance amplifier is nothing more then a voltage controlled current source (VCCS) the gain expression is \$g_m = \frac{I_{out}}{V_{in}} = \frac{dI_C}{dV_{BE}}\$

And for example, to find the output voltage in you amplifier circuit we can use a nodal analysis and write for the output node:

$$ \frac{V_{OUT}}{R_1} + g_m \cdot V_{IN} + \frac{V_{OUT} - V_{IN}}{R_2} = 0$$

And find the voltage gain is:

$$A_V = \frac{V_{OUT}}{V_{IN}} = - \frac{g_m R_1 R_2 - R_1}{R_1 + R_2} = -\frac{g_m R_1 - \frac{R_1}{R_2}}{1 + \frac{R_1}{R_2}} \approx - g_m R_1||R_2 $$

And to find the input resistance we can use the same approach and solve for

\$R_{IN} = \frac{V_{IN}}{I_{IN}}\$

But we also can use a Miller's Theorem

Miller's Theorem - Input Capacitance

And find \$R_{IN}\$ by inspection

$$R_{IN} = \left(\frac{R_2}{1 + |A_V|} \right)||\: r_{\pi} = \frac{R_2 r_{\pi}}{R_2 + (1 + |A_V|)r_{\pi}}$$