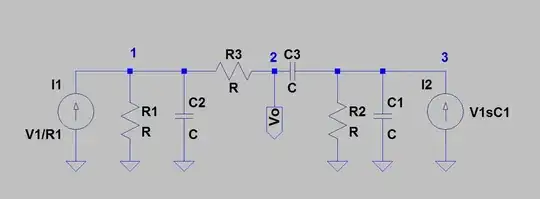
This is the circuit I am currently analyzing: (link to LTSpice file)
I am trying to predict each stage closed loop gain and overall gain (with all loops closed).
First thing I did is calculate DC conditions in circuit for given parameters and then started dealing with feedback of each circuit. Also, at beginning, I connected each sub-circuit separately to a source, to make things easier.

simulate this circuit – Schematic created using CircuitLab
FIGURE A:
\$r_e = 43\Omega\$, \$\beta = 250\$, \$I_c = 600 \mu A\$, \$r_\pi = 10.8k\Omega\$, \$A_{ol} = 387\$
\$r_e = 26mV/I_e\$, \$r_\pi = r_e *(\beta + 1)\$, \$A_{ol} = \frac{(R_2 + R_1||R_\pi)||R_3}{r_e}\$ (NFB loading included)
I defined closed loop equation from KCL $$ \frac{V_{IN}-V_B}{R_1} - \frac{V_{OUT}-V_B}{R_2} - \frac{V_B}{r_\pi} = 0 $$ and got
$$ A_{CL(Q1)} = \frac{V_{OUT}}{V_{IN}} = \frac{R_2}{R_1} - \frac{V_B R_2(R_2 r_\pi - R_1 r_\pi + R_1 R_2)}{V_{IN}R_1 R_2 r_\pi} = 30.4 $$
In LTSpice I measured \$ \frac{V_{OUT}}{V_{IN}} = 30.3 \$, so I got pretty close with upper equation.
FIGURE B:
\$r_e = 43\Omega\$, \$\beta = 250\$, \$I_c = 592 \mu A\$, \$r_\pi = 66.2k\Omega\$, \$A_{ol} = 63 \$
\$r_e = 26mV/I_e\$, \$r_\pi = (R_9+r_e) *(\beta + 1)\$, \$A_{ol} = \frac{(R_7 + R_1||R_\pi)||R_5}{(R_9+r_e)}\$ (NFB loading included)
I defined closed loop equation from KCL $$ \frac{V_{IN}-V_B}{R_1} - \frac{V_{OUT}-V_B}{R_7} - \frac{V_B}{r_\pi} = 0 $$ and got
$$ A_{CL(Q2)} = \frac{V_{OUT}}{V_{IN}} = \frac{R_7}{R_1} - \frac{V_B R_7(R_7 r_\pi - R_1 r_\pi + R_1 R_7)}{V_{IN}R_1 R_7 r_\pi} = 22.4 $$
In LTSpice I measured \$ \frac{V_{OUT}}{V_{IN}} = 21.3 \$. Not so close to calculated value as for Figure A, but close enough for me.
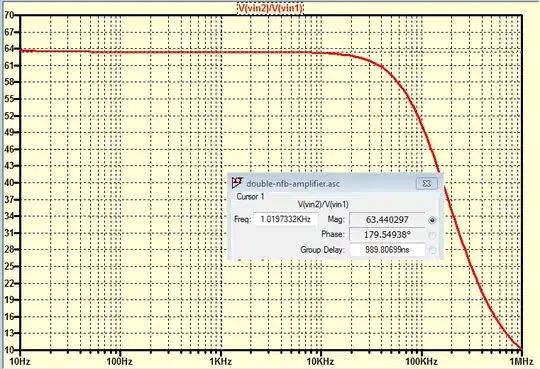
FIGURE C: (here things aren't as they should be - as was measured from LTSpice)
Main thing here was to predict overall gain of circuit from Figure C. I thought I would achieve this by multiplying each sub-circuits closed loop (active) gain and also multiplying each sub-circuit's input gain (passive - smaller than 1), which comes into place due to finite input resistance and non-zero output resistance of each BJT. Like so:
$$ A_{CL(OVERALL)} = A_{P(Q1)} * A_{CL(Q1)} * A_{P(Q2)} * A_{CL(Q2)} = 354 $$
where
$$ A_{P(Q1)} = \frac {r_{\pi(Q1)}}{R1+r_{\pi(Q1)}} = 0.65 $$ $$ A_{P(Q2)} = \frac {r_{\pi(Q2)}}{((R_2 + R1||r_{\pi(Q1)})||R3)+r_{\pi(Q2)}} = 0.80 $$
In LTSpice, I measured \$ A_{CL(OVERALL)} = 1135 \$. As you can see, measured value is at least 3x bigger compared to what I calculated! This is a huge difference that cannot be accepted. So, when both sub-circuits are combined, something happens that I didn't manage to predict. Something must greatly be wrong with my calculations, otherwise such enormous error wouldn't take place in this example.
Can anyone tell/explain me, where did I go wrong, when analyzing this specific circuit? Can anyone spot the mistake(s) I have made?