Note: this is part of a larger question which I was asked to separate into subquestions. Other subquestions: 1 and 2
I'm using the method outlined here to measure the induced magnetic flux density in a toroidal transformer made of Nanoperm (additional datasheets here and here). I am trying to adapt the method to use a passive integrator rather than the op-amp integrator described in the tutorial. (I tried building the active one but it was giving me issues.)
The diagram of my circuit is given below:
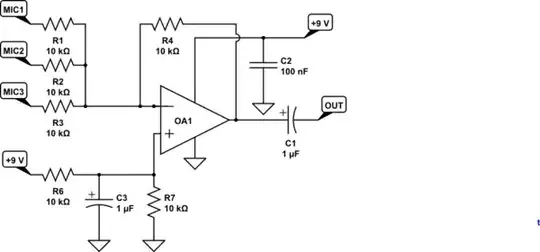
simulate this circuit – Schematic created using CircuitLab
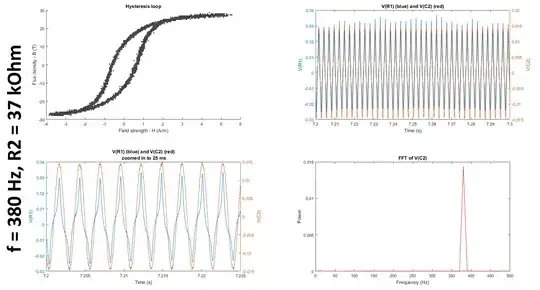
where I am varying the input frequency of V1 to be either 50 Hz (as reported in the datasheets to measure hysteresis), 350 Hz, and 380 Hz, and I am varying R2 to be either 5 kOhm, 10 kOhm, 27 kOhm, or 37 kOhm. Note that the signal generator is connected to an audio amplifier capable of driving large currents. A result from one of my experiments is shown here:
For more details about the experiment and results, please see my original larger question.
While the shape of the hysteresis loop looks somewhat similar to that of the loops reported in the data sheet, it is orders of magnitude off in terms of both H and B. I posted a related question about this possibly being attributed to the way I was calculating H and B and/or to the fact that the gain of the RC integrator at the frequencies I'm looking at being much less than 1. I'm also wondering, since I'm using a passive integrator, does the EMF induced in the measurement coil need to be buffered before being fed into the integrator?