25

I found them on www.digikey.com, and they're apparently made by different manufacturers, so there must be some use for them. What are they used for?

edit
and why? The 2400 baud modem doesn't offer an explanation: a 12 Mhz crystal is better for that than the 12.000393 Mhz.

Federico Russo
  • 9,658
  • 17
  • 68
  • 117
  • There're many other possibly interesting frequencies such as 2.097152, 3.342336, 4.194304, 4.433619, 8.867238, 12.865625, 17.734475, etc. Perhaps the question could be extended to include these (and maybe others that I've missed). – Thorn Aug 28 '12 at 14:35
  • @Thorn: but those don't have a close frequency as an alternative. The 12000393 is only 33 ppm from 12MHz, which even may be within tolerances. – Federico Russo Aug 28 '12 at 14:56
  • The (now deleted?) comment about DTMF frequencies seems a good fit - it means you need to create 8 frequencies for DTMF, and another 5 for the data transfer (1070/1270/1800/2025/2225 Hz), and all of them need to be 0.01% within spec... – hli Aug 28 '12 at 17:11
  • @FedericoRusso: In some cases, it may be necessary to have two frequencies which are close, but be certain that one of them is above the other. For example, the actual data modulation rate on a 1200-baud or 2400-baud modem is slightly above 1200 or 2400 baud; the modem will insert extra stop bits as needed when transferring data from the 1200 or 2400-baud RS-232 connection to the slightly-faster data modulator. Still, the modem's data modulation rate is more than 33ppm above the 1200 or 2400-baud nominal rate. – supercat Aug 28 '12 at 17:12
  • @hli - I commented to that deleted answer that the error of a 12 MHz crystal is less than 0.004 %, which is really negligible; those DTMF ICs used analog bandpass filters, they weren't anywhere so critical, certainly not the 0.01 % you claim. – stevenvh Aug 28 '12 at 17:56
  • @stevenh basic engineering practice would be for the detectors to be designed to accept a far wider range, with the transmitters required to produce within a much narrower one. – Chris Stratton Aug 28 '12 at 18:04
  • @Chris - Agreed, but what error level are we talking about: 33 ppm. A standard crystal at the time may have had a 50 ppm tolerance + tempco. – stevenvh Aug 28 '12 at 18:09
  • @stevenh - the DTMF frequencies have up (down?) to 1.5% accuracy - but the modem signals need to be much more accurate. V.29 states that the 1700Hz carrier frequency must not deviate more than 1Hz - which is 0.5% (which is still more than the 0.1% I intended to write instead of 0.01%...) – hli Aug 28 '12 at 20:19
  • @hli - If 0.5 % is required then I presume you agree a frequency deviating 0.003 % from 12 MHz is pointless? – stevenvh Aug 29 '12 at 12:02
  • @Thorn [This answer](http://electronics.stackexchange.com/a/5851/11864) has a good explanation of how Baud rates can result in those other odd frequencies. – alx9r Aug 29 '12 at 15:49
  • I could pull a crystal 400Hz with a load capacitor. It would be weird to sell a crystal like that, rather than saying "12.000MHz with 32pf load". But I've seen strange stuff issue forth from those who don't know their history. – gbarry Aug 29 '12 at 17:23
  • @stevenh - you are right. But the interesting part is that with such a crystal you can have all the modem and the DTMF frequencies too really close to where they should be (within 0.1Hz if I remember this comment right - did not check). My other guess (as commented below) would be that the actual implementation needs to ensure that the generated clock does not sync with the data clock, but is somewhat faster. – hli Aug 29 '12 at 18:04
  • @hli: Assuming that the 12.000393MHz clock is exact and that you divide it to slightly above 2400Hz, you are still not guaranteed that the clock is higher than the datarate. In asynchronous mode, the V.22bis specification requires the receiver to accept signalling rates between 2400 and 2455 bps. – jarnbjo Aug 30 '12 at 11:09
  • @jarnbjo - that's why I called it 'a guess'. Actually no-one of us here has any clue why it is so :( – hli Aug 30 '12 at 18:01

5 Answers5

4

Edit: After coming back to this question a week or so after the original post, I'm pretty sure that my answer here is incorrect. Please see the comments for the discussion. While most of the discussion is correct, my presumption in this answer about how frequency is specified by manufacturers seems to be incorrect. In particular, frequency is specified at the exact specified value of Cload, not at the mean frequency that can result from the range of tolerable C_load.

A crystal unlike an oscillator depends on user-provided load capacitance to determine its oscillating frequency:

Adding additional capacitance across a crystal will cause the parallel resonance to shift downward. This can be used to adjust the frequency at which a crystal oscillates. Crystal manufacturers normally cut and trim their crystals to have a specified resonance frequency with a known 'load' capacitance added to the crystal. For example, a crystal intended for a  6 pF load has its specified parallel resonance frequency when a 6.0 pF capacitor is placed across it. Without this capacitance, the resonance frequency is higher.

The capacitance tolerance range of the user-provided capacitance is centered around the capacitance's nominal value. The relationship between load capacitance and frequency, however, is not linear:

enter image description here

(For background info see the graph on page 4 and discussion on page 3)

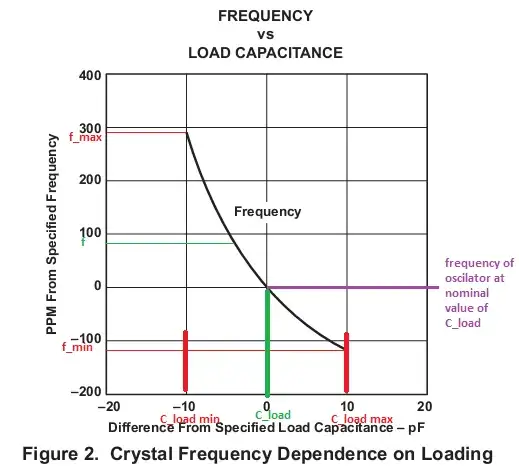
In figure 2,

  • f is the nominal crystal frequency (in green),
  • C_load is the nominal load capacitance (in green), and
  • min and max (in red) denote the minimum and maximums of tolerance ranges.

The result of the non-linearity is that the frequency at the mean of the tolerance range of the capacitance (the purple line) does not correspond with the mean of the frequency tolerance range f.

It is conventional for manufacturers to define nominal values of components as being the mean of their highest and lowest tolerable values given a list of conditions. The given conditions for the crystal in this case are C_load +/- tolerance.

Relative the frequency at the nominal load capacitance (the purple line), the lowest tolerable load capacitance C_load_min results in a higher frequency shift upward (to f_max) than does the highest tolerable load capacitance C_load_max cause a shift downward (to f_min). This means that the nominal value of the crystal frequency f --which is defined by convention to be the mean of the highest and lowest frequencies -- will be slightly higher than the frequency that results if the load capacitance is exactly the nominal value of the load capacitance (the purple line).

That slightly higher mean frequency is where the numbers after the decimal point come from in the nominal frequency of 12.000393 MHz.

Community
  • 1
alx9r
  • 258
  • 1
  • 7
  • According to this there shouldn't be crystal frequencies like 12.000 MHz, 4.000 MHz, 10.000 MHz, etc at all. They all should be 4.000123 MHz or 10.000456 MHz. – stevenvh Aug 29 '12 at 06:12
  • I still don't get it. When the mean frequency you get is _higher_ than the specified one, and you want to have, in most cases, the specified one, should the chosen crystal frequency be _lower_ than the one you need? If I want to get 12.000000 MHz, and be with in 50ppm or so, shouldn't I use a 11.999800 MHz crystal, so that my frequency range is somewhere between 11.999000 and 12.001000 MHz? – hli Aug 29 '12 at 18:14
  • Also, the frequency requirements of the chips mentioned above also gives this frequency as requirement when an external oscillator is used. So it doesn't seem to have to do with the frequency accuracy. – hli Aug 29 '12 at 18:15
  • @hli You make a good point and raised a whole other question: What is the meaning of the nominal frequency that manufacturers specify? Does the 16.000312 MHz frequency specified on the [RC224AT data](http://www.datasheetcatalog.org/datasheet/Conexant/mXvqysv.pdf) refer to the series resonant frequency? The antiresonance frequency? Or is it the Parallel resonant frequency given a particular load capacitance. That question is [here](http://electronics.stackexchange.com/questions/39098/what-is-the-meaning-of-the-nominal-frequency-specified-by-manufacturers-of-cryst). – alx9r Aug 29 '12 at 21:38
  • @hli I assume you are referring to the RC224ATL datasheet. That datasheet specifies a 16.000312 MHz crystal with 56 pF +/- 5% load capacitance. It does not specify a maximum or minimum input frequency to XTLI. – alx9r Aug 29 '12 at 21:41
  • @hli My first comment here was confusing and I don't think helpful or in the right direction. I've deleted it. This whole discussion hinges on the answer to [this question](http://electronics.stackexchange.com/questions/39098/what-is-the-meaning-of-the-nominal-frequency-specified-by-manufacturers-of-cryst). – alx9r Aug 29 '12 at 21:47
2

It seems to be used in old modems (up to 2400 baud it seems). I found several links describing the contents of old 2400 baud modems, and they all list such a crystal as component. But unfortunatley I have not found a circuit so far.

But I cannot see which target frequency it can create which a 12MHz crystal cannot (after all, 12MHz divided by 5000 is exactly 2400). I think the reasons are somewhere buried in the ancient modem standards (V.22bis and earlier), but for this you need someone who knows them by heart...

hli
  • 2,336
  • 15
  • 17
1

I don't know why such an odd frequency is required, but they are e.g. used to drive the Rockwell RC224AT/1 integrated modem chip.

jarnbjo
  • 221
  • 1
  • 5
  • Well, DSP can get weird. If it has anything to do with Bessel functions, the answer won't be posted by me :) – gbarry Aug 29 '12 at 17:19
1

Failure report:

So near, I thought, but still no cookie :-)

Manual and actually readable version of that circuit here but still no real clue. Note that crystal MAY be operated in 3rd (or other) overtone mode.

enter image description here

Russell McMahon
  • 147,325
  • 18
  • 210
  • 386
  • This doesn't seem like an answer, but figuring out how you tell the modem chip that it has a 12.000393 MHz crystal instead of a 16.000312 MHz might lead to a discovery. If this were a movie, there would be a quest to track down the guy who designed it... – Chris Stratton Aug 28 '12 at 18:01
  • @Chris - Not an answer, but it confirms the trend of the other answers (including your deleted one): this clearly is a modem thing! – stevenvh Aug 28 '12 at 18:12
  • The [RC224AT data sheet](http://www.alldatasheet.com/view.jsp?Searchword=RC224AT/1) has this on page 2-12. For each baud rate, the baud rate generator is programmed accordingly. A base frequency of 115200Hz is used, so with the 12MHz crystal, instead of a divider of 48 for 2400 baud, a divider of 36 must be used. – hli Aug 28 '12 at 18:13
  • @ChrisStratton - "This doessn't seem ..." -> That's why it's headed "Failure Report". The aim was to be useful. I added it as it adds to the body of knowledge so far, demonstrates where in a typical circuit such a xtal is used and provides a complete commerical modem circuit using one. A bit hard to fit into a comment. Sure, I could have left off the image, but it informs people well enough without having to dig. et al. Whatever. – Russell McMahon Aug 28 '12 at 19:08
  • Since there are many other modem implementations out there (even for the same V.x standards) which use proper frequencies (meaning with integer dividers to the desired frequencies), I think it has more to do with the actual implementation, instead of being a general requirement. It might be that it requires the clock signal to be slightly out of sync with the processed signals (e.g. you sync on a start frame, and when the next start frame arrives you are in the middle of a clock period, and not on a clock edge). But this also is just a guess. – hli Aug 28 '12 at 20:11
0

The answer seems to be boring: they are set to those specific frequencies to ensure that they are >=12.000000mhz over their entire temperature range.

Myforwik
  • 697
  • 1
  • 5
  • 12
  • 2
    Why would that be necessary? Wouldn't it be better to have tolerances plus and minus, so that the maximum deviation is less? – Federico Russo Sep 07 '12 at 12:54