Circuit for Inverse Chebyshev or Elliptic LPF

Question

I know I came across a 2 op-amp, 2 capacitor circuit that can be used for a single section of an Inverse Chebyshev (a.k.a. "Chebyshev Type II) or an Elliptic (Cauer) filter. It has a pair of zeros on the \$j\omega\$-axis at \$\pm j\omega_z\$, and with resonant frequency \$\omega_0<\omega_z\$ and the transfer function is:

$$ H(s) = \frac{1 + \left(\tfrac{s}{\omega_z}\right)^2 }{1+\tfrac{1}{Q}\tfrac{s}{\omega_0}+\left(\tfrac{s}{\omega_0}\right)^2} $$

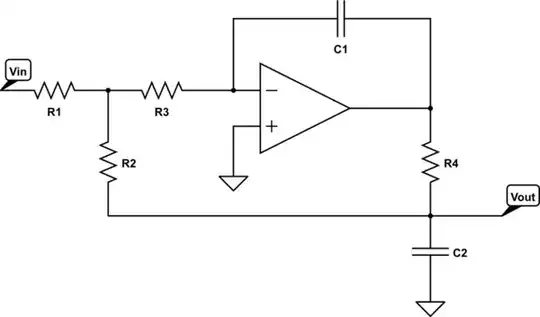
I know how to brute force derive a circuit with a pair of integrators and the canonical form we learned in Linear Circuits class 4 decades ago. Such as this:

I just thought I saw a more elegant circuit, with one less op-amp and a couple fewer resistors, that pretty much guaranteed that the zeros lie on the \$j\omega\$-axis and at a higher frequency than the resonant frequency \$\omega_0\$. Anybody know how to save a couple of parts with this? Is there a single op-amp, two-capacitor, 4-resistor circuit that can do this?

A sorta Sallen-Key with zeros.

I'm so ashamed of myself. 4 decades ago, I would know this. But I can't remember this now. — robert bristow-johnson, Aug 02 '18 at 07:55

score 3 · Accepted Answer · edited Feb 26 '22 at 23:20

3

There are several one-opamp circuits with Chebyshev II or Cauer behaviour, for example:

double-T-feedback circuits with positive (fixed) gain,
Boctor-filter (based on Multi-feedback topology),
Scultety-structure
GIC-based structures

(Hint: Google for Boctor and Scultety)

For example, see here:

http://www.schematica.com/active_filter_resources/a_list_of_active_filter_circuit_topologies.html

edited Feb 26 '22 at 23:20

Nicolas

200
1
11

answered Aug 02 '18 at 09:32

LvW

24,857
2
23
52

my goodness, what a useful link! i had never heard of schematica.com before. – robert bristow-johnson Aug 02 '18 at 17:23
looks to me that the Boctor might be the one. (i don't want more storage elements than the order of the filter, so the double T is less preferred.) – robert bristow-johnson Aug 02 '18 at 17:25
Yes - another point: Double-T is very sensitive to component tolerances (exact matching required). In this respect, GIC structures are best - however with two opamps. – LvW Aug 03 '18 at 07:31

score 0 · Answer 2 · answered Aug 02 '18 at 08:08

0

I'm wondering, will this do it?

schematic

^{simulate this circuit – Schematic created using CircuitLab}

answered Aug 02 '18 at 08:08

robert bristow-johnson

1,645
1
12
29

doing the node-voltage method now. what an interesting trip down memory lane. – robert bristow-johnson Aug 02 '18 at 08:19
Why not simulate it? – Andy aka Aug 02 '18 at 08:19
i wanna transfer function. – robert bristow-johnson Aug 02 '18 at 08:20
Well you can try this circuit or that circuit and derive the TF for each and examine the TF to see if it matches or you can just mess around with a sim until you get the TF looking about right then derive it. It's your time you'll be spending. – Andy aka Aug 02 '18 at 08:21
i want something that relates R1, R2, R3, R4, C1, and C2 to \$Q\$, \$\omega_0\$, and \$\omega_z\$. – robert bristow-johnson Aug 02 '18 at 08:22
i just gotta slug out this node-voltage analysis. – robert bristow-johnson Aug 02 '18 at 08:22
Cascading a notch filter with a sallen key will do the job – Andy aka Aug 02 '18 at 08:22
two capacitors. – robert bristow-johnson Aug 02 '18 at 08:23
1

This opamp circuit only has one zero, so it can't realize the transfer function in the question. – Sven B Aug 02 '18 at 12:30
thanks for confirming what it appeared to me to be, @SvenB. – robert bristow-johnson Aug 02 '18 at 17:46

Circuit for Inverse Chebyshev or Elliptic LPF

2 Answers2