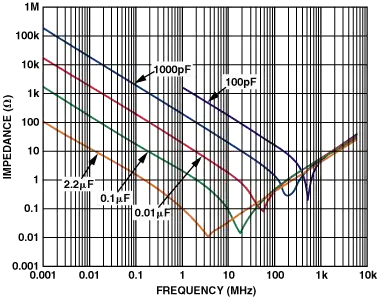
This effect is due to the effects of parasitic characteristics of the device. A capacitor has four basic parasitics:
Equivalent Series Resistance - ESR:
A capacitor is really a capacitor in series with the resistances of its leads, the foil in the dielectric, and other small resistances. This means that the capacitor cannot truly discharge instantly, and also that it will heat up when repeatedly charged and discharged. This is an important parameter when designing power systems.
Leakage current:
The dielectric is not ideal, so you can add a resistance in parallel with your capacitor. This is important in backup systems, and the leakage current of an electrolytic can be much greater than the current required to maintain RAM on a microcontroller.
Dielectric Absorption - CDA:
This is usually of less interest than the other parameters, especially for electrolytics, for which leakage current overwhelms the effect. For large ceramics, you can imagine that there is an RC circuit in parallel with the capacitor. When the capacitor is charged for a long period of time, the imagined capacitor acquires a charge. If the capacitor is rapidly discharged for a brief period and subsequently returned to an open circuit, the parasitic capacitor begins to recharge the main capacitor.
Equivalent Series Inductance - ESL:
By now, you shouldn't be too surprised that, if everything has capacitance as well as nonzero and non-infinite resistance, everything also has parasitic inductance. Whether these are significant is a function of frequency, which leads us to the topic of impedance.
We represent impedance by the letter Z. Impedance can be thought of like resistance, just in the frequency domain. In the same way that a resistance resists the flow of DC current, so does an impedance impede the flow of AC current. Just as resistance is V/R, if we integrate into the time domain, impedance is V(t)/ I(t).
You'll either have to do some calculus, or buy the following assertions about the impedance of a component with an applied sinusoidal voltage with a frequency of w:
\$
\begin{align}
Z_{resistor} &= R\\
Z_{capacitor} &= \frac{1}{j \omega C} = \frac{1}{sC}\\
Z_{inductor} &= j\omega L = sL
\end{align}
\$
Yes, \$j\$ is the same as \$i\$ (the imaginary number, \$\sqrt{-1}\$), but in electronics, \$i\$ usually represents current, so we use \$j\$. Also, \$\omega\$ is traditionally the Greek letter omega (which looks like w.) The letter 's' refers to a complex frequency (not sinusoidal).
Yuck, right? But you get the idea - A resistor doesn't change its impedance when you apply an AC signal. A capacitor has reduced impedance with higher frequency, and it's nearly infinite at DC, which we expect. An inductor has increased impedance with higher frequency - think of an RF choke that's designed to remove spikes.
We can calculate the impedance of two components in series by adding the impedances. If we have a capacitor in series with an inductor, we have:
\$
\begin{align}
Z &= Z_C + Z_L\\
&= \frac{1}{j\omega C + j\omega L}
\end{align}
\$
What happens when we increase the frequency? A long time ago, our component was an electrolytic capacitor, so we'll assume that \$C\$ is very much greater than \$L\$. At first glance, we'd imagine that the ratios wouldn't change. But, some trivial (Note: This is a relative term) complex algebra shows a different outcome:
\$
\begin{align*}
Z &= \frac{1}{j \omega C} + j \omega L\\
&= \frac{1}{j \omega C} + \frac{j \omega L \times j \omega C}{j \omega C}\\
&= \frac{1 + j \omega L \times j \omega C)}{j \omega C}\\
&= \frac{1 - \omega^2 LC}{j \omega C}\\
&= \frac{-j \times (1 - \omega^2 LC)}{j \omega C}\\
&= \frac{(\omega^2 LC - 1) * j)}{\omega C}
\end{align*}
\$
Well, that was fun, right? This is the kind of thing you do once, remember the answer, and then don't worry about it. What do we know from the last equation? Consider first the case where \$\omega\$ is small, \$L\$ is small, and \$C\$ is large. We have, approximately,
\$
\begin{align*}
\frac{(small * small * large - 1) \times j}{small * large}
\end{align*}
\$
which is a negative number (assuming \$small * small * large < 1\$, which it is for practical components). This is familiar as \$Z_C = \frac{-j}{\omega C}\$ - It's a capacitor!
How about, second, your case (High-frequency electrolytic) where \$\omega\$ is large, \$L\$ is small, and \$C\$ is large. We have, approximately,
\$
\begin{align*}
\frac{(large * small * large - 1) \times j}{small * large}
\end{align*}
\$
which is a positive number (assuming \$large * small * large > 1\$). This is familiar as \$Z_L = j \omega L\$ - It's an inductor!
What happens if \$\omega^2 LC = 1\$? Then the impedance is zero!?!? Yes! This is called the resonant frequency - It's the point at the bottom of the curve you showed in your question. Why isn't it actually zero? Because of ESR.
TL,DR: Weird stuff happens when you increase the frequency a lot. Always follow the manufacturers' datasheets for decoupling your ICs, and get a good textbook or take a class if you need to do high speed stuff.