Simple circuit, mesh method, can't resolve

Question

I'm trying to resolve this for 3 hours now, I think I made some errors around the last part but can't figure out where.

I'm a beginner and I'm still learning.

If you want to try here is the circuit:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

I start by making 3 equations, put them in matrix form, make the inverse of the R matrix.

So in the start I had: $$R * I = V$$ With the inverse matrix I'll have: $$I = V * R^-1$$

In order to find \$R^-1\$ I'm using the formula: $$1/detR * (R^a)^T$$ Where \$R^a\$ is the matrix formed by "algebraic complements" and \$(R^a)^T\$ is the transposed one.

The exercise requires to find the \$Vx\$ in \$R5\$ and basically to find everything... So:

\$Pg1 = ?\$

\$Pg2 = ?\$

\$I1, I2, I3 = ?\$

\$Vx = ?\$

(Vx as I said is the Voltage in R5 and Pg1, Pg2 is the Power delivered/absorbed by the generators)

Don't know how to put them in here in a mathematical form, I'll try but between "$" doesn't work. — AlexanderWalls, Jul 04 '18 at 17:12
You can learn to use it [here](https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference) or use alternative methods. We can't help you find error in equations without seeing them. — Eugene Sh., Jul 04 '18 at 17:14
Please also show the matrices you obtained from the equations. — Elliot Alderson, Jul 04 '18 at 17:18
I don't know if MathJax is implemented here, seems it doesn't recognize the "$" at all. I'll try with a photo... — AlexanderWalls, Jul 04 '18 at 17:19
Do you have to solve it this way or are other methods allowed? — Andy aka, Jul 04 '18 at 17:27
Isn't Cramer's rule usually taught for this, when doing it by hand? — jonk, Jul 04 '18 at 17:33
@neilpare Your equations look fine to me, first blush (I do the signs exactly the opposite, but it results in the same as what you have.) Your matrix looks laid out right to me. And I get results for all three currents, which are sensible. So it's your processing to get the values that is problematic. Are you using Cramer's rule? Or what? A tool to invert R? What exactly is giving you poor results? — jonk, Jul 04 '18 at 17:40
Use matlab or similar to invert the matrix and compare the results — Eugene Sh., Jul 04 '18 at 17:57
I used Sarrus to find detR, I'm adding details, I had to go before but now I'm finishing the question :) (sorry) — AlexanderWalls, Jul 04 '18 at 18:12
After the edits, this is what a great homework question looks like. Also how a great "new user" reacts to constructive criticism - adding the missing stuff instead of arguing! — pipe, Jul 04 '18 at 19:27
Thanks to everyone for the support! I tried a similar exercise after and resolved it in 15 minutes :) — AlexanderWalls, Jul 05 '18 at 12:31

jonk · Accepted Answer · 2018-07-04T20:59:33.463

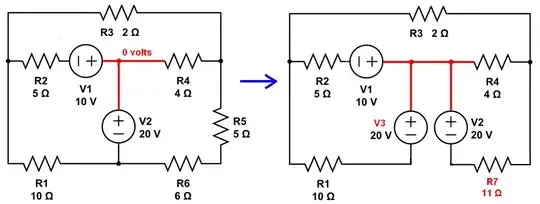
Your schematic and the current directions I chose to take in my own head:

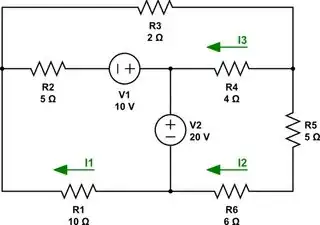
schematic

^{simulate this circuit – Schematic created using CircuitLab}

I get the same equations you do. My work is on the left, and yours (or closer to yours) is on the right:

$$\small\begin{align*} -I_1\:R_1 - \left(I_1-I_3\right)R_2+V_1-V_2 &=0\:\text{V} & I_1\:R_1 + \left(I_1-I_3\right)R_2 &=V_1-V_2\\\\ V_2-\left(I_2-I_3\right)R_4-I_2\left(R_5+R_6\right) &= 0\:\text{V} &\left(I_2-I_3\right)R_4+I_2\left(R_5+R_6\right)&=V_2\\\\ -V_1-\left(I_3-I_1\right)R_2-I_3\:R_3 -\left(I_3-I_2\right)R_4&=0\:\text{V} & \left(I_3-I_1\right)R_2+I_3\:R_3 +\left(I_3-I_2\right)R_4&=-V_1 \end{align*}$$

These result in the same matrix you formed:

$$\left[\begin{array}{ccc} R_1+R_2 & 0 & -R_2\\\\ 0 & R_4+R_5+R_6 & -R_4\\\\ -R_2 & -R_4 & R_2+R_3+R_4 \end{array}\right]\left[\begin{array}{c}I_1\\\\I_2\\\\I_3\end{array}\right]=\left[\begin{array}{c}V_1-V_2\\\\V_2\\\\-V_1\end{array}\right]$$

If you want to solve this by hand, Cramer's rule is often taught. Here:

$$\tiny\begin{align*} I_1 &= \frac{\text{det}\left[\begin{array}{ccc}V_1-V_2 & 0 & -R_2\\ V_2 & R_4+R_5+R_6 & -R_4\\ -V_1 & -R_4 & R_2+R_3+R_4\end{array}\right]}{\text{det}\left[\begin{array}{ccc}R_1+R_2 & 0 & -R_2\\ 0 & R_4+R_5+R_6 & -R_4\\ -R_2 & -R_4 & R_2+R_3+R_4\end{array}\right]}& I_2 &= \frac{\text{det}\left[\begin{array}{ccc}R_1+R_2 & V_1-V_2 & -R_2\\ 0 & V_2 & -R_4\\ -R_2 & -V_1 & R_2+R_3+R_4\end{array}\right]}{\text{det}\left[\begin{array}{ccc}R_1+R_2 & 0 & -R_2\\ 0 & R_4+R_5+R_6 & -R_4\\ -R_2 & -R_4 & R_2+R_3+R_4\end{array}\right]}& I_3 &= \frac{\text{det}\left[\begin{array}{ccc}R_1+R_2 & 0 & V_1-V_2\\ 0 & R_4+R_5+R_6 & V_2\\ -R_2 & -R_4 & -V_1\end{array}\right]}{\text{det}\left[\begin{array}{ccc}R_1+R_2 & 0 & -R_2\\ 0 & R_4+R_5+R_6 & -R_4\\ -R_2 & -R_4 & R_2+R_3+R_4\end{array}\right]} \end{align*}$$

So have you tried this approach?

A recent paper, A condensation-based application of Cramer’s rule for solving large-scale linear systems, Habgood & Arel, Journal of Discrete Algorithms 10, 2012, pp. 98–109, demonstrates that Cramer's rule can perform on the same computational order as other methods, such as LU decomposition. Nice to read about that.

Assuming you've worked out the three currents above, you can now easily work out the magnitude of the voltage across \$R_5\$ (if I understood your use of \$V_x\$, correctly) and you can work out its polarity with respect to the presumed current, \$I_2\$, as well.

I think you know how to calculate the current in \$V_1\$ as the sum of two of the three currents you worked out above. And similarly, for \$V_2\$. From those currents and the known voltages of each, you should have no trouble working out the power they contribute (the sign telling you if they are generating (-) or dissipating (+) power.)

These last details shouldn't be difficult, once you have the three currents worked out.

No I didn't, my last brain cell remained after those 3 hours didn't remembered Cramer. So I made the inverse of the R matrix and found I1,2,3 manually. The problem I had was in the resulted power generated by V1 and V2. Thanks anyway for the excellent answer! — AlexanderWalls, Jul 04 '18 at 18:48
@neilpare Just got back from work and noticed your comment. I'm not sure what part of your edited question you want addressed any further. I gather that you've figured out the values for the three currents? — jonk, Jul 04 '18 at 19:53
Yeah I added some details just to let you know, your answer gave me another important point of view. Cramer was a win here and surely I'll remember to use it the next time :) thanks so much for the great work! :) — AlexanderWalls, Jul 05 '18 at 12:29

score 5 · Answer 2 · answered Jul 04 '18 at 17:59

5

If you want to try here is the circuit:

Firstly, try and look at things as an EE would. For instance I could convert your diagram like this: -

Note that mentally I've named a node as 0 volts because it makes sense to me but it isn't an important thing to do if you don't want to do this. Then I've split V2 into two occurances (V2 and V3) so that I can disconnect the net between R1 and R6. I've also combined R5 and R6 into R7.

What I'd do next is make V1 and R2 into a 2 amp current source in parallel with R2 and make V3 and R1 into another 2 amp current source in parallel with R1.

Those two parallel current sources make 4 amps across 3.333 ohms (R1 || R2). I can then convert back to a common voltage source of 13.333 volts in series with 3.333 ohms and the job is looking a lot simpler: -

Next I would convert V2 and R7 into a current source of 1.818 amps in parallel with R7 and this then is placed in parallel with R4. Combine R4 with R7 and convert back to a voltage source and you are at the important point of calculating the current through R3. From hereon in it becomes a case of using R3's current to help solve the more localized voltages on nodes.

answered Jul 04 '18 at 17:59

Andy aka

434,556
28
351
777

Wow man, great job I didn't think about this solution. Anyway I don't like in general to change the circuit, it's too mechanic and also it requires time, that I will not have in the exam lol *The exercise requires to solve the circuit and find I1, I2, I3 and the V in every resistor.* – AlexanderWalls Jul 04 '18 at 18:05
That's the way I'd do it in an exam because it builds on sensible (to me) steps and in virtually three little hand sketches and a few words I've got you I3 (assuming that is the current thru R3). – Andy aka Jul 04 '18 at 18:27
@neilpare I would also note that splitting V2 like that is also known as "source shifting". Might come in handy on your exam. – Sven B Jul 04 '18 at 18:32
@SvenB I didn't know it had a name!! – Andy aka Jul 04 '18 at 18:37
Question edited :) – AlexanderWalls Jul 04 '18 at 18:49

Simple circuit, mesh method, can't resolve

2 Answers2