0

I am being asked to find the output resistance of the current mirror below. the correct answer is supposed to be R_out = 103k ohms. but when am simulating the circuit, I get R_out = 3.82k ohms. Can somebody please help me and tell what wrong is going on???? Btw, R_s in the circuit diagram is 3k ohms. Here is the problem statement along with the simulation results.

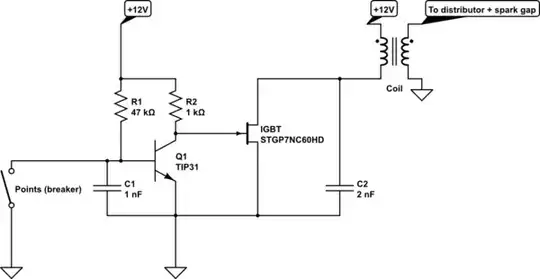
problem schematic

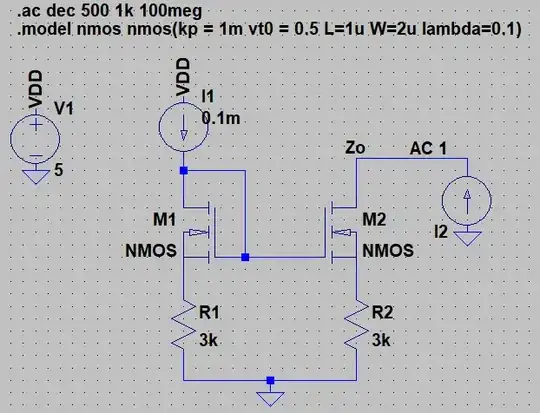
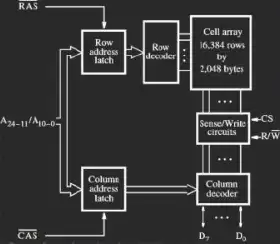
enter image description here

enter image description here

Thank you for your help.

JordenSH
  • 299
  • 1
  • 3
  • 14
  • How did you select your NMOS model? Were no specs given for the FETs? Or is the model shown the model you have to work with? Lambda will have a strong influence on your output resistance. – John D Jun 12 '18 at 16:20
  • these values are common for a mosfet and they don't change the outcome significantly. what matters is the ro which comes from VA = 10V and ID is obviously 0.1mA – JordenSH Jun 12 '18 at 16:30
  • 1
    A typical example of a GIGO. If you do not know how to use a circuit simulator do not use it. As hint LTspice first computes the dc operating point and then the AC analysis is launched. What is M2 DC drain current? – G36 Jun 12 '18 at 16:32
  • 2
    OK, glad to hear that lambda won't influence your results, it's only VA that will have an effect. Oh, wait...... – John D Jun 12 '18 at 16:47

3 Answers3

2

The one way of finding the\$R_{OUT}\$ resistance in a proper way is shown here:

enter image description here

enter image description here

And what you should know that the LTspice first computes the dc operating point and then based on this result (gm, ro) the AC analysis is performed.

All this means that if you include \$\lambda\$ in your MOSFET model. You no longer can assume that \$I_{D1} = I_{D2}\$ and \$r_{o1} = r_{o2}\$

Because the lambda will also affect the DC-operating point also.

And the equation for \$R_{OUT}\$ is \$R_{OUT} = ro2*(1+gmR_S)+R_S \$

I/O Resistance of common source MOSFET with source degeneration

G36
  • 13,642
  • 1
  • 18
  • 33
  • This is the correct answer. You will get 103K if you remove the source degeneration resistors, but the negative feedback they introduce raises the output impedance. Your original circuit, as G36 points out will open the AC current source load for DC operating point analysis forcing the output current to zero. The voltage source load is the right way to go. – John D Jun 12 '18 at 18:25
  • 1
    Yes of course, and sweeping the Voltage source affects the results slightly until it bottoms out of range. – Tony Stewart EE75 Jun 12 '18 at 18:43
1

I see you're utilizing the Sedra/Smith textbook on Microelectronics. So for this answer I'll be utilizing the 7th Edition of the book.

On page 513 in Chapter 8, you're given the basic structure of the current mirror. Notice how this picture below looks extremely similar to your picture.

enter image description here

There's a formula on that same page that will become very handy in what you're trying to solve for:

\$ \displaystyle R_o=r_{o2}=\frac{V_{A2}}{I_o}=\frac{\Delta V_o}{\Delta I_o}\$

where \$r_o\$ is your small signal output resistance and \$V_A\$ is your early voltage. Early voltage can also be described as \$V_A = 1/\lambda_n\$.

It is also important to note that when you're solving for your output voltage it should be the following criteria: \$V_o \geq V_{GS}-V_{tn}\$

Going on to the next page, it'll tell you how the equation for the output current:

\$ \displaystyle I_o=\frac{(W/L)_2}{(W/L)_1}I_{REF}(1+\frac{V_o-V_{GS}}{V_{A2}})\$

Since you're talking about current mirrors, I presume that you can take it from here with circuit analysis. Only difference now is that there are resistors in your problem. But again, with circuit analysis you'll be able to solve this. As far as your simulation, I agree with what @JohnD commented above. Make sure you have your proper specifications for your NMOS devices. I recommend solving this by hand as this looks like a homework problem and your professor probably wants you to show your work.

  • This is not a homework problem. I am doing this for my own knowledge. Furthermore, the circuit analysis by hand is already done and as I stated in my question the answer should be 103k ohms. What I want to do is to prove the hand analysis using LTSpice simulation tool. Since you are familiar with Sedra Smith textbook please refer to problem 8.54 of the 7th edition. – JordenSH Jun 12 '18 at 16:45
  • 1
    @Raykh If you are doing this for your own knowledge who is asking you? "I am being asked to find the output resistance of the current mirror below." As you know by now your hand calculation is only correct without source degeneration resistors. – John D Jun 12 '18 at 22:44
1

I believe it is your test method that is wrong.

Using a current source to drive a current sink (mirror) without a proper quiescent point in the linear range is likely to drive the FET into conduction.

So you are seeing the sum of RdsOn and Rs rather than the high impedance you expect from a controlled current sink.

\$ \displaystyle R_o=r_{o2}=\frac{V_{A2}}{I_o}=\frac{\Delta V_o}{\Delta I_o}\$. (With boundaries on Io since this is a voltage controlled mirror.

Try again.

One way to measure impedance is to use a current source, but not on a current sink as you must match them perfectly to prevent Vds going to 0 or Vdd.

Consider a swept DC voltage source with a swept AC f and measure the change in Io then compute as per equation above to see when it changes. The tolerance range of Vds vs the tolerance of Ro as a ratio is called the Sensitivity factor and with a defined tolerance you can express the useable range of Vds.

Then consider the test you chose used an ideal current source fighting against a non-ideal current sink to understand why it failed.

Tony Stewart EE75
  • 1
  • 3
  • 54
  • 182