You are right about this \$ 5\tau\$. It takes about \$ 5\tau\$ to fully charge the capacitor. But fully charged means here \$0.993V_{CC} \approx V_{CC} = 12 \textrm{V}\$
And it seems that you forget that to open the bipolar transistor you need only \$0.5\textrm{V}... 0.6\textrm{V}\$ across the base-emitter junction.
So, in reality, your transistor will be long open after this \$ 5\tau\$.
The voltage across the capacitor versus time in \$RC\$ circuit describe this equation:
$$V_C(t) = V_{CC}(1 - e^{\frac{-t}{RC}})$$
And we need to find how long it takes to charge the capacitor to about \$0.6\textrm{V}\$
So, we need to solve for \$t\$
$$V_C = V_{CC} \cdot (1 - e^{\frac{-t}{RC}})$$
$$\frac{V_C}{V_{CC}} = 1 - e^{\frac{-t}{RC}}$$
$$\frac{V_C}{V_{CC}} -1 = - e^{\frac{-t}{RC}}$$
$$ 1 - \frac{V_C}{V_{CC}} = e^{\frac{-t}{RC}}$$
$$ \frac{1}{1 - \frac{V_C}{V_{CC}}} = e^{\frac{t}{RC}}$$
$$ \frac{1}{\frac{V_{CC}-V_C}{V_{CC}}} = e^{\frac{t}{RC}}$$
$$ ln\left(\frac{1}{\frac{V_{CC}-V_C}{V_{CC}}}\right) = {\frac{t}{RC}}$$
$$ ln\left({\frac{V_{CC}}{V_{CC}-V_C}}\right) = {\frac{t}{RC}}$$
And finally, we have:
$$ t = RC\cdot ln\left({\frac{V_{CC}}{V_{CC}-V_C}}\right) = 60 \textrm{k}\Omega \cdot 10\mu \textrm{F}\cdot ln\left({\frac{12\textrm{V}}{12\textrm{V}-0.6\textrm{V}}}\right) = 30.78 \textrm{ms} $$
As you can see you need to increases the circuit time constant.
But increasing the resistance \$R\$ is not a good idea. Because in your circuit BJT's must work as a switch. Hence the base current must be larger then \$Ib>> \frac{I_C}{\beta}\$ to make sure that the BJT's enters the saturation region. Where \$I_C\$ is collector current in this circuit it's a relay current and \$\beta\$ is a minimum beta value.
Bjt base current calculation
I do not know the relay current so I can't help here.
The simples solution to this problem will be adding another BJT as a Darlington stage or even a Zener diode in series with the base. Or use a MOSFET instead of a BJT.
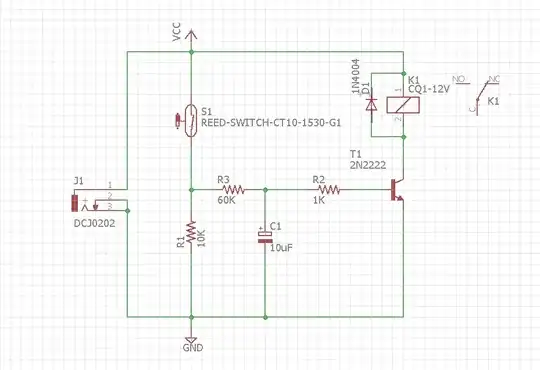 Here I have a design ( Vcc = 12V ) where relay gets activated whenever reed switch gets closed. I want to activate the relay after a delay of about 2 to 3 seconds from the instant reed switch gets closed.
Here I have a design ( Vcc = 12V ) where relay gets activated whenever reed switch gets closed. I want to activate the relay after a delay of about 2 to 3 seconds from the instant reed switch gets closed.