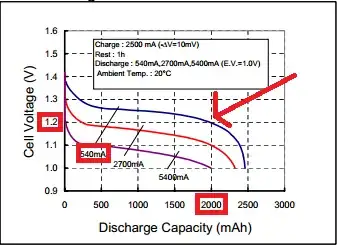
I'm dealing with the measurement of impedance sweeping the frequency from 0,1Hz to 100KHz. On the web I found many methods but the most quoted seems to be the one which uses an operation amplifier in inverting low-pass filter configuration:
Z represent the impedance under test. In this configuration, we can find the module and phase of Z comparing the input and the output of the filter.
Another simplest method I found is the common voltage divider:
Z is the impedance under test again and its module and phase can be found again comparing the input and the output signals.
Now, I know that the first method which uses the opamp should be the better choice since it's used in the most Z-meter, but I don't understand the real advantage using that one.
Can anyone light up my mind?