Understanding memory requirements for an image file

Question

I want to understand the memory requirements for image resource files to be displayed on a 240x400 resolution display.

The display has the following specs:

It supports upto 18 bits color depth and uses ILI9327 display driver.

Assuming that I need to display 50 different icons, each of size 10 mm X 10 mm, what is the storage space required?

Here are my calculations:

Pixels per mm = 400/61.2 = 6.536

Number of pixels in one image = 65.36 x 65.36 = 4272 pixels

Each pixel will require 18 bits X 3 (for R, G and B) = 54 bits

Total bits required = 4272 x 54 = 230688 bits = 28.16 kilobytes

For 50 images, I will require 1.375 megabytes of storage.

Is my calculation correct?

Answer 1

Pixels per mm = 400/61.2 = 6.536

Yup.

Number of pixels in one image = 65.36 x 65.36 = 4272 pixels

Well, you mean pixels per icon. But even so, you cannot produce fractional pixels, so your number should either be 65 x 65 or 66 x 66. And this leads to a further simplification. Why not make your icons 64 x 64? This will simplify address calculations for your memory, and will only produce a "shrinkage" of about 2%. And trust me, at this size nobody will notice. Then your icons will be 4096 pixels in size.

Each pixel will require 18 bits X 3 (for R, G and B) = 54 bits

Nope. As jms just answered, it's 18 bits per pixel total, or 6 bits per color. Again, though, you should consider not worrying quite so much about the bit level. Store your color values as partial bytes (6 bits per byte) with separate bytes per color. This will take 33% more memory, but will drastically reduce your processing load when transferring from memory to screen.

Total bits required = 4272 x 54 = 230688 bits = 28.16 kilobytes

Total bits is 4096 x 24, or 98304 bits, or 12288 bytes.

For 50 images, I will require 1.375 megabytes of storage.

12288 times 50 gives 614400 bytes.

Answer 2

Make life simple for yourself by making the icons 64×64 pixels. Draw a border around them if you want them to look larger.

With the 16-bit color format, this only requires 8 kB per icon, or 400 kB for the set of 50.

One simple form of compression is to use a color table instead of storing every pixel's color directly. 16 colors is frequently more than enough for an icon, especially if you apply a little creative dithering. This reduces the storage to 2 kB per icon, plus 32 bytes for the color table. Total storage is a little over 101 kB if every icon has its own color table.

---

Just to satisfy my own curiosity, I grabbed the following "worst case" image (from here):

This ImageMagick command line

convert image.jpg -crop 267x267+66+0 -resize 64x64 -colors 16 final.png

turned it into this:

Not bad, and of course source images with a more limited range of colors will come out even better. For example, here's Olin, processed the same way:

Answer 3

More about color depth

Expanding on Dave Tweed's answer, you can do even better than what he showed.

Here is the same large-size original he used:

Cropped to be square and shrunk to 64 x 64 pixels but using full (8 bit per red, grn, blu) color yields:

Rounding the color information from 8 bits per channel to 6 bits results in:

That is what your display can do, since you say it supports 18 bit color depth.

Rounding the color information further to 5 bits for red, 6 for green, and 5 for blue, for a total of 16 bits/pixel yields:

This really should be plenty good enough for icons.

Even without any compression, icons of this format take only 64 x 64 x 2 = 8192 bytes. 50 such images would require 409,600 bytes.

Answer 4

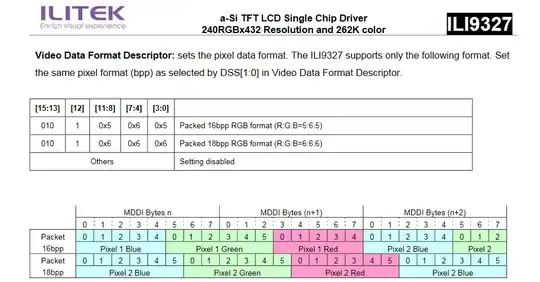
Each pixel will require 18 bits X 3 (for R, G and B) = 54 bits

Your estimate is incorrect. The "18 bits" value is per pixel, not per colour. The red, green and blue channels each have a maximum bit depth of 6 bits (64 different values), 18 bits in total.
This display controller also supports a 16-bit mode (where pixel data only has 5 bits for red, 6 for green and 5 for blue) which makes it easy to pack each pixel into just two bytes. This makes it easier to store bitmaps efficiently and increases the amount of pixels you can write to the display per second.

Number of pixels in one image = 65.36 x 65.36 = 4272 pixels

You can't practically store fractional pixels, so your actual bitmaps (images/sprites/characters/whatever) would probably be 65² = 4225 pixels.

Going the easy route (16-bit R5G6B5 pixel format), 4225 * 16 bits would amount to 67600 bits per bitmap, or 8450 bytes per bitmap. 50 images would require 423 kB (with no compression).

If you really want the full colour depth, you need more than 2 bytes per pixel. At that stage you might just as well devote one byte for each colour (as WhatRoughBeast suggests), which will further inflate the storage requirement by 3/2 (634 kB for 50 65x65 bitmaps).

You could also pack the 18-bit pixels right next to each other in memory (subpixel bits unaligned with byte boundaries), without wasting any bits. You would only need 476 kB for the 50 65x65 18-bit bitmaps, but it would be a pain to program and slower to process.