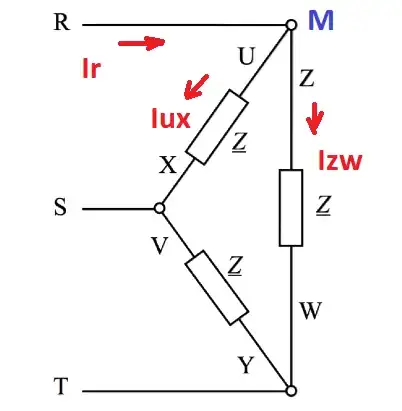
Below is a 3-phase delta connected for balanced loads Z:
Since phase-to-phase voltages (voltage across loads) have 120 degrees phase differences and since the loads have the same impedance we can conclude that the currents Iux, Izw, Ivy across the loads also must have 120 degrees phase difference with the same RMS values. So one can draw the phasor for these currents as:
I'm experiencing some confusion for writing the node currents as KCL. For example, take node M above in my first drawing.
Vectorially for the currents at node M which one is correct and why?
Ir = Iux + Izw ?
Ir = Iux - Izw ?
According to what I read Ir must be sqrt(3) times the load current, but I don't know how they derive this by using KCL considering the phasor diagrams.