2

Full disclosure, I've asked a very similar question before which didn't have much success as it was too specific. However I want to try again by restricting the scope of the question.

Scenario

I'm performing measurements of a transfer function of a DAQ (NI USB-6251). I have placed 2 MΩ in series between the input and output of the DAQ:

schematic

simulate this circuit – Schematic created using CircuitLab

The output/input impedances in the above schematic come from the DAQ datasheet.

Due to the 100 pF at the input to the DAQ I expect to see a low pass filter with cutoff frequency at $$ \frac{1}{2\pi (2\times 10^6)(100\times10^{-12})} = 795\ \text{Hz} $$

Measured results

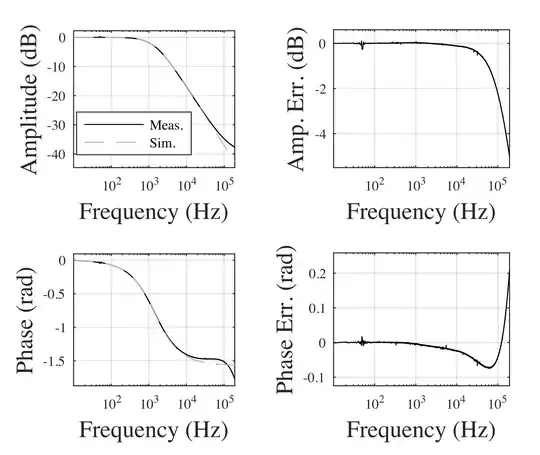
enter image description here

Fitting an RC model to the measurements I find the capacitance to be around 57 pF (1396 Hz 3 dB point). This then fits quite well to the measurements, up to about 10 kHz.

The question

Why at high frequencies do the measurements deviate from the model? Has anyone seen this behaviour before?

Edit

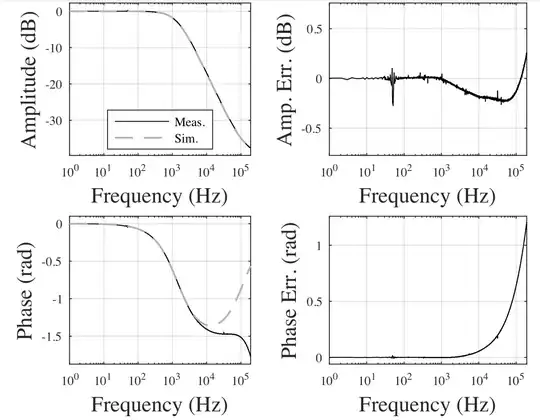
Below is the measurement with no R2, i.e. no 2 M resistor. There still seems to be a deviation in amplitude and phase from the anticipated flat response. The amplitude response fits what is specified in the datasheet in Figure 2.

For reference, I'm using a sample rate of 1 MHz, am using a signal length of 1 second which is averaged 100 times. enter image description here

Edit 2

I have updated my model: it now actually includes the 0.2 Ω output resistance, and now includes a parasitic capacitance across the resistor. Hand-tuning using the amplitude response, I found 650 fF to be a good fit, illustrated in the figure below. While the phase is over-compensated I am beginning to see that this is likely in higher-order parasitic effects as was mentioned by Daniel Turizo in my previous question. It does not look like it will be easy to get a perfect fit at higher frequencies, particularly because I am working on a breadboard...

enter image description here

loudnoises
  • 1,816
  • 16
  • 28
  • It looks like the zero with the 650fF is set, all that's needed is the higher frequency pole to curb down the response. Maybe that's inside the box (most probably, inherent poles). – a concerned citizen Apr 22 '18 at 13:03
  • @aconcernedcitizen could you please expand on what you mean by inherent poles? – loudnoises Apr 22 '18 at 14:51
  • 1
    I mean similar to an opamp, limited bandwidth, maybe due to parasitic capacitances, inductive traces, etc. Otherwise having a zerowould mean clear derivative from that point to light. – a concerned citizen Apr 22 '18 at 16:07

2 Answers2

2

Simulate a parasitic capacitance (say 0.1pF or 0.5pF) in parallel with your 2M resistor and see what happens.

1

First of all, thank you for asking such a specific question. I see a lot of questions here that are just homework related.

I am not sure but I think this systematic error is because of high frequency coupling. Your 2M source impedance is so big that the source to the input of the DAC is very weak. Radio waves tend to couple better with higher frequency. That‘s what I see from your figures: In real, you measure more signal amplitude with higher frequency than simulated.

Stefan Wyss
  • 6,471
  • 1
  • 11
  • 22
  • Thank you for your answer! I was interested in what you said about the 2 M impedance, so I have repeated the measurement without the resistor to see what happens. It still shows deviation from what I expect. Does this correspond with what you meant by the radio interference? – loudnoises Apr 22 '18 at 11:31
  • 1
    Well, you did not show the simulation results and honestly I can’t see any deviation from what I would expect. The amplitude seems to be flat up to the new cutoff frequency which is somewhere at 1MHz. What is it that puzzles you about this measurement result? – Stefan Wyss Apr 22 '18 at 12:48
  • Yep you're totally right, I forgot about the spec'd frequency response of the DAQ illustrated in the datasheet, Figure 2. – loudnoises Apr 22 '18 at 13:05