3

I designed this class A amplifier. It's my first attempt at designing an amplifier with transistors. My objective is to build a guitar amplifier with tubes, but I figured that building an amp with BJTs and a low-voltage power supply first will enable me to understand what's going on before I attempt anything more complicated.

I want to drive an 8-ohm speaker. The problem, of course, is that if I connect RS, the speaker, suddenly the AC signal sees basically 8 ohms to ground and can't develop any voltage at the Q1 collector.

I think that the proper way to do this is to connect the Q1 collector to the base of another transistor, Q2, configured as an emitter follower, and drive the speaker from the emitter of Q2.

But what I'd like to understand is, what is the limiting factor that prevents me from driving the speaker from Q1? I have a fuzzy understanding that I need Q1 to provide voltage amplification and then an emitter follower to provide the current to drive the speaker, but I don't understand why I can't get both in one place, since all the power is ultimately coming from the same power supply. Is there a way to enable this circuit to drive an 8-ohm speaker without adding a second transistor?

schematic

simulate this circuit – Schematic created using CircuitLab

Willis Blackburn
  • 1,217
  • 1
  • 13
  • 24
  • 1
    C3's a whopper ain't it? – Paul Uszak Apr 14 '18 at 21:58
  • 1
    Let's say the output resistance of your amplifier is 300 ohms. And that it outputs Vmax volts. How many volts will you be able to see on a 8 ohms load? (Do you see a voltage divider realized with Rload and Rout?). Well the reason you can't do it with one stage is that: the CE (with emitter degeneration) has a good amplification but also a medium sized Rout. So, if your load does not match that Rout you need something else to match it. – Sredni Vashtar Apr 14 '18 at 22:43
  • The way this was done with vacuum tubes (if class-A) was to swing the plate (or cathode, sometimes) voltage around over a very large voltage range and to feed that (several different ways) through a transformer that dropped the high voltage swing while increasing the current compliance. In effect, the transformer matched the speaker impedance to the tube circuit impedance (which is often in the vicinity of \$6\:\text{k}\Omega\$.) Your BJT collector can pull down. But it can't "pull up." The only thing pulling up is \$R_L\$. Not going to work. – jonk Apr 14 '18 at 22:52
  • (Just noticed you called RL what I call Rc - which is basically Rout - and Rs what I call RLoad). How much can you lower your RL (my Rout) and your Re to keep the gain? – Sredni Vashtar Apr 14 '18 at 22:52
  • How did you come up with this design in the first place without considering the effect of the load impedance? If you need a complete course in common-emitter amplifier design, this question is far too broad for this site. – Dave Tweed Apr 14 '18 at 22:57
  • Why don't you just put your schematics into LTspice, and look at all waveforms (voltages and currents) by yourself? – Ale..chenski Apr 14 '18 at 23:02
  • As with any Class A Amp. Your load impedance must be > Rc to prevent starving the Ic current. So you cannot drive 8 with 330 Ohms. Remember the collector is a current source. transistor radios with only 7 BJTs in total would use a step down transformer to isolate DC from speaker and transform the impedance. – Tony Stewart EE75 Apr 14 '18 at 23:38
  • 2
    @Dave Tweed, sorry I must have slipped and typed "I need a complete course in common-emitter amplifier design," when what I meant was, "is it possible to modify this design to drive the speaker from Q1," my apologies. – Willis Blackburn Apr 14 '18 at 23:43
  • And yet you couldn't answer my question. If you want help here, lose the attitude and be more cooperative with the volunteers who are trying to assist you. – Dave Tweed Apr 14 '18 at 23:48
  • @SredniVashtar thanks for your explanation, I'm getting that there's just no good way to drive a heavy load in the common emitter configuration, unless I'm willing to push a huge amount of current through Q1 as the answer below suggests. – Willis Blackburn Apr 15 '18 at 00:59
  • Q1, if properly chosen and heatsinked could withstand the current. It's the coil running with 750mA DC that would be a problem for me (but I'm no audiobuff) – Sredni Vashtar Apr 15 '18 at 01:04
  • @PaulUszak that seemed to be about right given the 28-ohm resistor. 100uF cuts off a little higher but would also work. Do you think I calculated it incorrectly? – Willis Blackburn Apr 15 '18 at 01:07
  • 1
    I just skimmed through it, but you could try something like this: https://www.youtube.com/watch?v=cbc3Q-AGOJM but the resistors and the heatsink will cost you more than another stage (also with a gain of 10 instead of 30). Also, you could follow Jonk's suggestion and get hold of a transformer, like here: https://www.youtube.com/watch?v=WXNGB3BjVvA – Sredni Vashtar Apr 15 '18 at 03:32
  • I just viewed both of @SredniVashtar 's videos. Egads! It's irksome enough to make me do a class-A design. I'll go with the \$12\:\text{V}\$ rail, single supply, class-A operation, \$8\:\Omega\$ speaker impedance, and set it for \$1\:\text{W}\$ output. AC gain of 15. Feel free to chip in or tear it apart. – jonk Apr 15 '18 at 05:53
  • @jonk those are basically the exact parameters I was going for, so please let me know how you make out. I started out selecting the quiescent collector current. The tutorial I was reading suggested "10-20% of the transistor's maximum current" but then said that 1mA was common. I went with 10%, about 20mA. But if it's going to drive a high-impedance power stage then maybe 20mA is too high. The R values all seem low compared with other schematics I've seen. – Willis Blackburn Apr 15 '18 at 13:39
  • @jonk Nevermind, just saw your new answer, can't wait to read it! – Willis Blackburn Apr 15 '18 at 13:40
  • @WillisBlackburn You would be a lot better off with a class-AB amplifier design. But there's more parts. See: [definition of amplifier operation classes](https://electronics.stackexchange.com/questions/364315/confusion-between-class-b-and-class-ab-amplifier/364320#364320). I'll add a class-AB amplifier design at the bottom of my answer, but I won't add a walk-though. The answer is already long enough. – jonk Apr 15 '18 at 18:53
  • @jonk I know that a class AB will be more efficient, but I'm new to this, and so I'm trying to implement the simplest thing that could possibly work to start. My main takeaway from this so far is that the 2N3904 is too wimpy to drive a speaker. If Q1 can amplify the incoming signal to about 8V p2p, call 3V RMS, then to drive an 8-ohm speaker I'd need 375mA right? That would get me about 1 watt of output power. But the 2N3904 can't deliver 375mA so I need something bigger. – Willis Blackburn Apr 15 '18 at 19:57
  • 1
    @WillisBlackburn The class-AB will be more efficient. The problem with discrete BJTs is that they vary one to another and they are affected by temperature. I'd hoped to walk you though a design process that get's close (but it's still "hobby level".) A single BJT amplifier does work but as you can see the videos they include a lot of heavy iron and/or BIG resistors. And they aren't good for the BJT, either. And the quality of the audio has a lot to be desired. – jonk Apr 15 '18 at 20:06
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/76071/discussion-between-willis-blackburn-and-jonk). – Willis Blackburn Apr 15 '18 at 20:29
  • @Jonk Well, it appears that was the scope of the question, right? Understanding the origin of the single bjt ampli limitations. I love your walkthroughs, but if we have to go to AB - something like this http://conradhoffman.com/papers_lib/AN485.pdf - then why not using an IC like the LM386 or a NE5532 and be done with? :-) – Sredni Vashtar Apr 15 '18 at 20:29
  • @SredniVashtar Yup. I'm with you entirely on that point. Partly, my reasoning is that I don't really know where the OP wants to go. Sometimes, it's a good idea to provide a large context out of which the OP can then work out what's important to them. But yeah, this is getting far afield. Granted. – jonk Apr 15 '18 at 20:42
  • The main thing that I take away from this question and it's contributors is: don't use transistors to amplify nothin'. Use op amps. – Paul Uszak Apr 15 '18 at 22:55
  • @PaulUszak You cannot avoid the final section. Where are you going to find an opamp capable of driving 200 W into an 8 ohm speaker? But I agree about much of the rest. (Except also for the pre-amp stages -- sometimes noise or special handling of the transducer cannot be handled with an opamp.) What goes on in the middle is probably opamp domain. – jonk Apr 16 '18 at 01:55
  • You have a voltage divider with 330 ohms and 8 ohms. The voltage across both, combined, is 12 volts. Calculate the voltage across the 8 ohm resistor. – user253751 Apr 16 '18 at 03:28
  • After studying this for a long time, I think that the answer is this: Driving a 4-ohm speaker requires something like 1000X the power that an electric guitar can generate, and getting 1000X amplification with one BJT is impossible. – Willis Blackburn May 14 '18 at 01:11
  • It can be done if you provide enough collector current. There are a number of amateur class A amplifies working on this principle without a buffer relying only on a feedback to provide low output impedance. Usually they employ a constant current source as a load and a shunt (collector to base) feedback. – e_asphyx Jul 24 '22 at 11:52

2 Answers2

5

It can be done. Remove Rs and C2. Let your speaker be RL. RE1 and RE2 should be smaller, because they seriously limit the voltage swing over RL.

Prepare to waste continuously about 9W, half of it in the speaker and possible RE and the other half in Q1 if you want the maximum theoretical audio output power. I bet 2N3904 doesn't stand one second, you need something stronger and well cooled.

ADD due the comments:

12V supply allows about 6V peak voltage swing. The DC resistance of the 8 Ohm speaker is near 8 Ohms. Let's assume it is 7 Ohm. Some RE is useful for linearity and thermal stability. Let's have one RE, only 1 Ohm. Now we have 6VDC over 8 Ohms.That means current =750mA. That means 9W DC power outtake from 12V in idle state.

The speaker should stand 750mA DC if it can handle say 10Watts.

Constructions like this were used by hobbyists in the old days (say 1960 - 1970) because they could get a couple of watts acceptable audio signal AC power without complex push-pull stages and the continuous power loss wasn't a problem if one used 12V car battery as his power supply. A 20cm x 20cm x 4mm aluminium heatsink was able to keep the transistor cool enough. The price of the transistors and other components is today so low that it's useless to avoid the normal push-pull output stage. Even class A amp works best as push-pull.

One trick: Put a massive inductor in parallel with the speaker. The DC current does not go through the speaker and you can multiple the output AC power, because the voltage swing can be more than 12Vpp. The inductor should be about 50 mH or more and it's iron core should be large enough to stand the DC magnetization without getting saturated.

In theory you can add a DC saturation compensating winding to the same inductor core if you drive the compensating DC through another speaker to pick the outputted AC. Otherwise it's a shorted transformer.

Another way to compensate is to add a permanent magnet to the magnetic circuit.

  • It occurred to me that I could put the speaker in place of RL, but in order to drop 6V across it, I'd need 750mA of current, which would fry the transistor. Did you get to 9W as 6V*0.75A? – Willis Blackburn Apr 15 '18 at 00:48
  • 3
    @WillisBlackburn You really aren't going to want a constant DC bias current in the speaker, itself. The idea of a speaker as the collector load isn't a good idea. – jonk Apr 15 '18 at 00:56
  • @WillisBlackburn the answer is augmented –  Apr 15 '18 at 05:51
  • @jonk I augmented my answer due the comments. –  Apr 15 '18 at 06:58
  • Just noticed my elementary math error above... I mean 9W = 12V*0.75A... – Willis Blackburn Apr 15 '18 at 13:44
5

Class-A amplifier design overview

After watching those two videos, Single transistor, 1W and Adventures in a one transistor audio amplifier, I had to illustrate a slightly more sane design approach. To start out, here's the basic idea about how to drive a speaker (without having to find and use a flux-limiting, gapped, audio transformer -- which you will definitely need if you plan to run DC current through the primary):

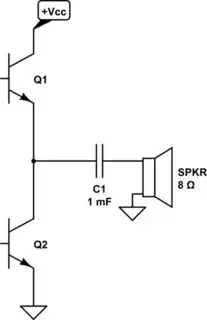
schematic

simulate this circuit – Schematic created using CircuitLab

\$Q_1\$ is an emitter follower and it will be able to source current into the speaker. \$Q_2\$ is a common emitter and it will be able to sink current from the load. Together, they can do a fair job of sinking and sourcing current.

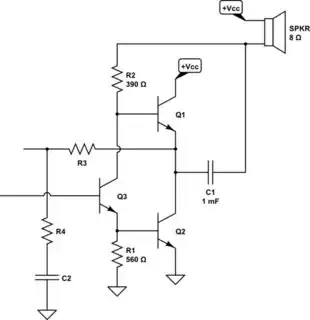
A 3rd BJT provides the voltage difference required:

schematic

simulate this circuit

Note that I've shown two schematics.

On the left, I've connected the speaker slightly differently (which would also work fine) in order to help segue into the transition on the right. I've also added the 3rd BJT that's needed. On the left is also a current source above \$Q_3\$ and a small resistor to sink a little excess current.

On the right, I've bootstrapped the design to provide the current source indicated on the left. Capacitor \$C_1\$ will develop a voltage across it that remains fairly fixed. Also, \$Q_1\$'s \$V_\text{BE}\$ will have a relatively fixed voltage across it, too. As a consequence, resistor \$R_2\$ will have a nearly fixed voltage across it. So it will form the equivalent of a constant current source. Just what we needed.

Class-A amplifier design details

The design is already taking shape. But it's time to put some parameters into it. In this case, \$V_\text{CC}=12\:\text{V}\$ (in keeping with one of the videos.) I'd like to leave about \$1.5\:\text{V}\$ \$V_\text{CE}\$ headroom for the two BJTs, \$Q_1\$ and \$Q_2\$, to keep them out of saturation and having some decent \$\beta\$ left over. This means that I've got about \$12\:\text{V}-2\cdot 1.5\:\text{V}=9\:\text{V}\$ of remaining swing feeding into \$C_1\$. So \$V_\text{PEAK}=\frac{9\:\text{V}}{2}=4.5\:\text{V}\$, or \$V_\text{RMS}=\frac{V_\text{PEAK}}{\sqrt{2}}\approx 3.2\:\text{V}\$.

The maximum power into the speaker will then be about \$\frac{V_\text{RMS}^2}{8\:\Omega}\approx 1\frac{1}{4}\:\text{W}\$.

We can estimate the peak current to the speaker now as \$\frac{4.5\:\text{V}}{8\:\Omega}\approx 560\:\text{mA}\$. \$Q_2\$ will have to sink that much current, plus some added current to stay in class-A operation. Let's set this minimum to about \$100\:\text{mA}\$. So the peak collector current for \$Q_2\$ (and the peak emitter current for \$Q_1\$) will be about \$660\:\text{mA}\$. Assuming an active \$\beta=60\$ (we can achieve that), this means the peak base currents will be on the order of \$11\:\text{mA}\$.

At this point I'm going to select the D44H11 BJT in the TO-220 package, knowing that I'm going to burn a watt or two in each. From the datasheet I estimate a peak \$V_\text{BE}\approx 800\:\text{mV}\$. I'd like to sink about \$1.5\:\text{mA}\$ with \$R_1\$, so this suggests \$R_1=\frac{800\:\text{mV}}{1.5\:\text{mA}}\approx 533\:\Omega\$. So I'll set \$R_1=560\:\Omega\$.

I will want the needed \$11\:\text{mA}\$, plus this added \$1.5\:\text{mA}\$, in \$R_2\$. So \$R_2=\frac{6\:\text{V}-800\:\text{mV}}{11\:\text{mA}+1.5\:\text{mA}}=416\:\Omega\$. I'll set it a little hotter to \$R_2=390\:\Omega\$.

Let's update the schematic:

schematic

simulate this circuit

NFB will be required to linearize the output and to set the AC gain. So I've added that feedback network above, with the addition of \$R_3\$, \$R_4\$, and \$C_2\$. I'm going to choose an AC gain of \$15\$, so \$R_3=15\cdot R_4\$.

Since \$Q_3\$ kind of makes up a Darlington with \$Q_2\$, the base current required for \$Q_3\$ will be on the order of \$\frac{13\:\text{mA}}{\beta=150}\approx 90\:\mu\text{A}\$. (It will often be less, but this is safe.) So this means I want a collector current for the fourth BJT to be about 10X more, or about \$1\:\text{mA}\$. \$C_2\$ just needs to be "big enough." I could get into the details to show that \$1\:\mu\text{F}\$ might be fine. But let's make it 10X bigger. So \$C_2=10\:\mu\text{F}\$.

Let's plug in the 4th BJT so that we can discuss the above details in a better light:

schematic

simulate this circuit

Now you can see that I've already put in values for the AC gain resistors and \$R_5\$ (newly added here.) I did this by recalling that I mentioned above that the collector current for \$Q_4\$ should be \$1\:\text{mA}\$. If you recall, I figure that the center voltage feeding into \$C_1\$ will be a quiescent \$6\:\text{V}\$. I'd like to drop about half that across the \$V_\text{CE}\$ of \$Q_4\$ and the rest I split evenly between \$R_3\$ and \$R_5\$. So those values are set. And since the gain is 15, the value of \$R_4\$ is also thereby set, too. As shown on the above schematic.

The only remaining problem is biasing \$Q_4\$. You can see in the above schematic that I've added a few parts to achieve that. Since \$Q_4\$'s collector current is about \$1\:\text{mA}\$, the base current will be well under \$10\:\mu\text{A}\$. I decided to choose about \$80\:\mu\text{A}\$ for the biasing current in \$R_6\$ and \$R_7\$, to make it stiff enough. I need a base voltage for \$Q_4\$ of about \$6\:\text{V}-1.5\:\text{V}-70\:\text{mV}=3.8\:\text{V}\$. So \$R_6=R_7=\frac{3.8\:\text{V}}{80\:\mu\text{A}}\approx 47\:\text{k}\Omega\$.

\$C_4\$ gives me an AC ground for a balanced midpoint. The only remaining thing is to compute \$R_8=\frac{12\:\text{V}-3.8\:\text{V}}{80\:\mu\text{A}}-R_6=55.5\:\text{k}\Omega\$. So \$R_8=56\:\text{k}\Omega\$.

Here's the final schematic:

schematic

simulate this circuit

That's a class-A amplifier, educational-level not professional.

(Update: I've added a necessary compensation pole capacitor, \$C_5\$, to the above circuit with a nominal value I think will be about right. It was important in order to roll off the high frequencies. So it's included now.)

I promised to add a class-AB. There are some tweaks needed to deal with discrete BJTs that haven't been included, nor discussions about them. So again, this is more of an educational level -- though if you built it I expect you'd still get passable results from it.

schematic

simulate this circuit

It includes temperature and device \$\beta\$ and \$V_\text{CE}\$ matching compensation for the diff-amp and mirrors and a few other areas, as well. Adjustments available for the VBE multiplier so that the quiescent current can be set up where you want it and so that the parabolic thermal response can be tweaked, as well.

jonk
  • 77,059
  • 6
  • 73
  • 185
  • Are you sure about the thermal stability? Nothing sees the current growth straight down through Q1 and Q2. –  Apr 15 '18 at 06:13
  • @user287001 True. I was hoping to avoid adding too much time to the design. If you want to add a suggestion, with quantitative calcs for it, I'll gladly add any good ideas you want. I've put as much time as I wanted and I'm already worried the OP won't follow. Meanwhile, I just ran a simulation with the BJTs (Q1 and Q2 only) set to boiling temperature (and leaving the others at about 35 C) and it barely moved. – jonk Apr 15 '18 at 06:21
  • Then you can say "I have simulated it. It's stable if you do not let it get over 100 degrees centigrade." –  Apr 15 '18 at 06:25
  • @user287001 If the OP shows further curiosity, I may add something. This illustrates a quick walk-through. (Like with coding, examples illustrate. Professional code does more, but often is harder to read for it.) – jonk Apr 15 '18 at 06:40
  • @jonk you made a John Linsley Hood class A amplifier from 1969. http://andijahja.com/jlh/index-1.htm – G36 Apr 15 '18 at 09:40
  • @G36 Well, it just took a few moments to do. I was barely thinking as I wrote. I'm in bed now and can't look at the link yet. The only weird thing I did was to add R8 so I could set the bias separately from the input loading. How close are the values? Was bootstrapping used too? Everything? Or just similar? It can't match everywhere! That would be crazy. – jonk Apr 15 '18 at 10:11
  • The original design 10W of a output power and use more traditional bootstrap circuit (two resistors) and R8 is also present. http://andijahja.com/jlh/jlh1969.pdf (page 7) – G36 Apr 15 '18 at 10:20
  • Thanks, @jonk. I do have some questions but I haven't watched the videos yet so maybe I can find answers there. – Willis Blackburn Apr 15 '18 at 14:04
  • @G36 Wow! I have a LOT to read there. Thanks!!! – jonk Apr 15 '18 at 18:46