Fourier series of output voltage

Question

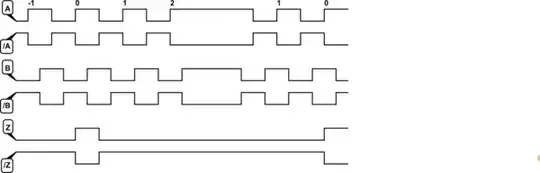
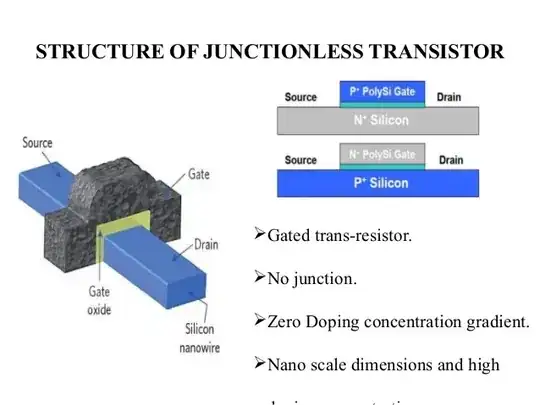
I've been practicing some Fourier series questions and then verifying my answers by generating an equivalent graph on MATLAB and comparing it with the graph generated by PSpice in simulating the same circuit.

This is my working:

The Fourier series of the source current:

\$i_s\left(t\right)=1+\frac{4}{\pi}\sum_{n=1}^{\infty}{\frac{1-\left(-1\right)^n}{n}\sin{n\pi t}}\$

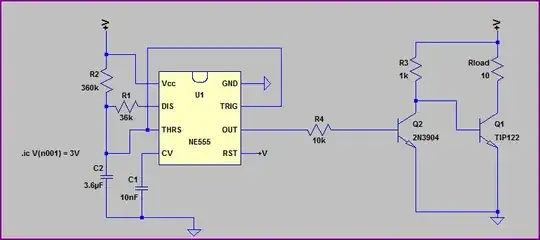
Then do a source transformation to simplify the circuit: \$v_s\left(t\right)=1i_s\left(t\right)\$

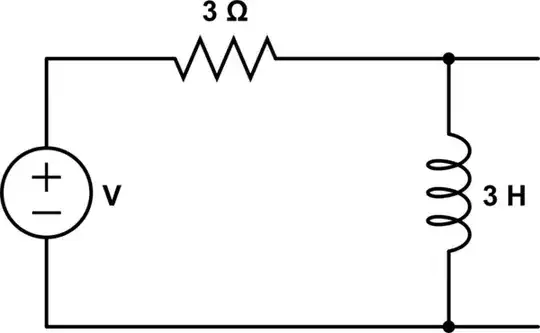
^{simulate this circuit – Schematic created using CircuitLab}

Then working in the phasor domain and using voltage division:

\$\omega_n=\pi n\$

\$V_{out}=\frac{Z_L}{Z_L+3}V_s\$

\$V_{out}=\frac{j\omega_n}{j\omega_n+1}V_s\$

\$V_s=I_s=\frac{4}{\pi n}\left(1-\left(-1\right)^n\right)e^{j\left(-90\right)}\$

\$V_{out}=\left(\frac{j\omega_n}{j\omega_n+1}\right)\left(\frac{4\left(1-\left(-1\right)^n\right)}{\pi n}\right)e^{j\left(-90\right)}\$

\$V_{out}=\left(\frac{4\left(1-\left(-1\right)^n\right)}{\pi n}\right)\left(\frac{w_ne^{j\left(90\right)}}{\sqrt{1+\omega_n^2}e^{j\left(\tan^{-1}{\pi n}\right)}}\right)e^{j\left(-90\right)}\$

Taking only odd n terms since evens result in 0:

\$V_{out}=\left(\frac{8}{\sqrt{1+\pi^2n^2}}\right)e^{j\left({-\tan}^{-1}{\pi n}\right)}\$

and finally in the time domain:

\$v_{out}\left(t\right)=\sum_{k=1}^{\infty}{\frac{8}{\sqrt{1+\pi^2n^2}}\cos{\left(\pi nt-\tan^{-1}{\pi n}\right)}}\$

with n = 2k - 1 for odd terms

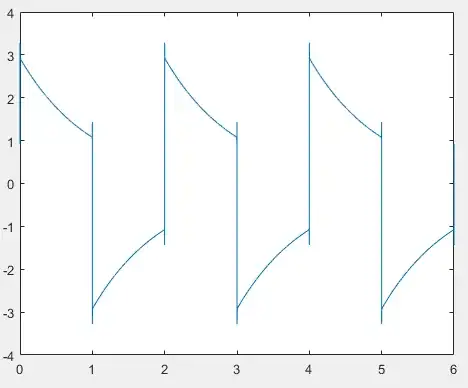
I plot my answer in MATLAB and it seems to be the negative of what the equivalent PSpice graph shows.

Can someone point out what is wrong please?

Answer 1

Your current source is referenced backwards. To demonstrate, try cutting the inductor out of the circuit and placing a probe on R2. This way, you'll just have a current source with a parallel resistor. In this case, it should be extremely clear that, when your current is positive, the voltage across your resistor should also be positive. I'm betting you'll see the opposite.

If I recreate the circuit, making sure the current source is referenced properly, I get your expected results:

Per your comment:

I don't think its inverted though, here is the graph with the current source added in. You can see it matches the graph in the question: i.imgur.com/Z7KiXDn.png

Try flipping the current source upside down and you'll still see the same current plotted (since your current probe will change directions too). That doesn't mean that the current is flowing in the direction that you're assuming it is. When you hover your mouse over the current source, you should be able to see the direction that the probe will assume (you'll want it pointing up).