This link states that when determining the power needed by an amplifier, you use the following formula:
I understand that the second term is due to the quiescent draw of the amp, but how is the first term derived? Where does the pi come from? I would have imagined it would be Vopeak^2 / R_L, since that is the peak power into the speaker.
Given \$\theta=\omega\:t=2\pi f t\$, just make \$\omega=1\$ for convenience.
Then \$\theta=t\$ and \$V_O=V_\text{PEAK}\cdot\operatorname{sin}\left(\theta\right)\$ and we can compute the upper quadrant power as:
$$\begin{align*} P_\text{UPPER}&=\frac{1}{2}\frac{1}{\pi}\int_0^\pi\left(V_\text{CC}-V_O\right)\frac{V_O}{R_\text{LOAD}}\:\text{d} \theta \end{align*}$$
The \$\frac{1}{2}\$ in front of that is because the power computation is for average power and the upper quadrant only operates for half of an entire cycle and will be zero power for the other half.
The lower quadrant will have the same figure as above (where \$V_\text{EE}=-V_\text{CC}\$.) So the total power of both quadrants added together is:
$$\begin{align*} P_\text{UP+LO}&=\frac{1}{\pi}\int_0^\pi\left(V_\text{CC}-V_O\right)\frac{V_O}{R_\text{LOAD}}\:\text{d} \theta\\\\ &=\frac{1}{\pi}\left[\frac{V_\text{CC}\cdot V_{PEAK}}{R_\text{LOAD}}\int_0^\pi \operatorname{sin}\left(\theta\right)\:\text{d} \theta-\frac{V_{PEAK}^2}{R_\text{LOAD}}\int_0^\pi \operatorname{sin}^2\left(\theta\right)\:\text{d} \theta\right]\\\\ &=\frac{1}{\pi}\left[\frac{V_\text{CC}\cdot V_{PEAK}}{R_\text{LOAD}}\cdot 2-\frac{V_{PEAK}^2}{R_\text{LOAD}}\cdot\frac{\pi}{2}\right]\\\\ &=\frac{2\cdot V_\text{CC}\cdot V_{PEAK}}{\pi \:R_\text{LOAD}}-\frac{V_{PEAK}^2}{2\:R_\text{LOAD}} \end{align*}$$
The power in \$R_\text{LOAD}\$ is obviously \$\frac{V_{PEAK}^2}{2\:R_\text{LOAD}}\$, so adding that to the above provides:
$$\begin{align*} P_\text{TOTAL}&=P_\text{UPPER}+P_\text{LOWER}+P_\text{LOAD}=\frac{2\cdot V_\text{CC}\cdot V_{PEAK}}{\pi \:R_\text{LOAD}} \end{align*}$$
The only remaining addition is to add the quiescent power and I think you already agreed about that part of the computation so I won't belabor it here.
Audio amplifiers typically operate in class-AB. Also read a very general description of the different classes of operation for an amplifier and the meaning of quadrant as I was using it above.
In class-AB, the basic amplifier block diagram would look something like this:
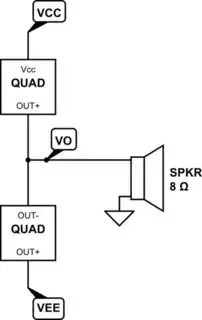
simulate this circuit – Schematic created using CircuitLab
From this, you can see that when \$V_O\$ is positive the lower quadrant is OFF and only the upper quadrant is ACTIVE. Similarly, when \$V_O\$ is negative the upper quadrant is OFF and only the lower quadrant is ACTIVE. To compute the average power for the upper quadrant, you have to take into account that it is only active for half a cycle. During the other half, it's OFF so there is no power dissipation during that half-cycle. So the average power for the upper quadrant over an entire cycle is one-half of the average power during its ACTIVE period. Similarly, for the lower quadrant.
Because it is class-AB and not precisely class-B, there is a quiescent current flowing between the upper and lower quadrants when \$V_O\approx 0\:\text{V}\$ (when there is no current in the speaker/load.) Since this current flows all the way through, from \$V_\text{CC}\$ to \$V_\text{EE}\$, you have to also account for that addition. There are several important reasons (cross-over distortion and thermal stability being a couple, but which may include others depending on the exact design) for including this quiescent current. It's not uncommon for this to amount to 5-10% of the rated power for the amplifier, but this percentage may also vary depending on the maximum power rating too since there are several factors being accounted for and no simple rule to follow. Regardless, it's worth accounting for it.
