We were given the following question in our circuit theory class:
Find the relation between \$R,L,C\$ such that the net reactance across terminals \$A\$ and \$B\$ is \$R\$.
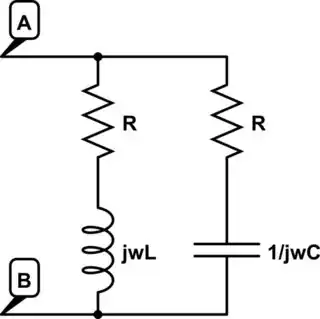
simulate this circuit – Schematic created using CircuitLab
I followed the generic method (equivalent parallel reactance):
$$\frac{1}{R}=\frac{1}{R+j\omega L} + \frac{1}{R+\frac{1}{j\omega C}}$$ to get the required relation (after eliminating \$\omega\$).
Upto that is okay. But I'm confused about something:
Suppose the system is inside a black box, with only terminals \$A\$ and \$B\$ outside. In that case how can we possibly distinguish between a black box containing this circuit vs. a black box which contains only a resistance \$R\$?