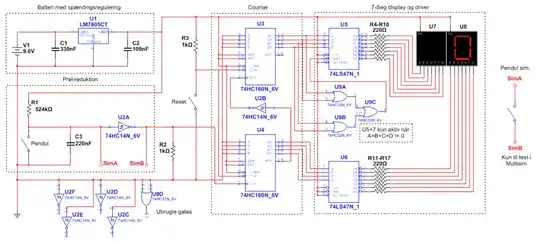
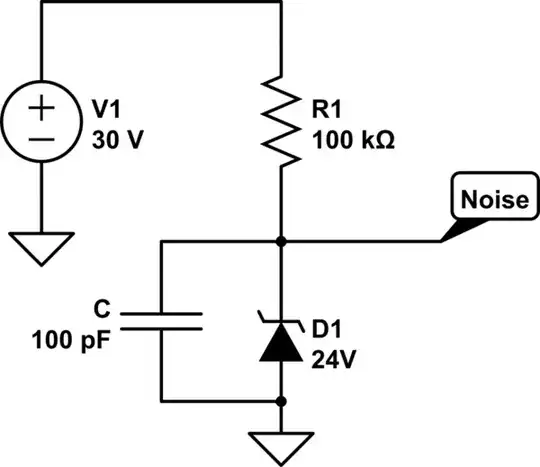
I have the following schematic of a Zener based noise source:-
simulate this circuit – Schematic created using CircuitLab
When built, an oscilloscope reveals a saw tooth noise signal at the "Noise" node, like:
The time base is 1us/div. Can anyone explain why the signal is saw tooth shaped? Initially I expected a triangular, or even sine shaped wave form. I think that it's something to do with the impedance of the Zener in conjunction with the much higher 100 kOhm resistor. The electrons cascade freely across the junction, but the resistor restricts current flow when the avalanche stops. We're talking 60uA. The result being slower charge build up than when current flows during avalanche.
This wave form isn't particular to my set up. There are other examples elsewhere on the Interweb when people have really zoomed in on the signal, one being https://youtu.be/CAas_kbTW3Q?t=714. Also there's a good chart here showing the rising edge to be slightly curved. It's probably unfamiliar as it's usually shown with a much slower time base. Am I right about the resistance/impedance explanation?