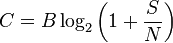1

Imagine a step response of a series RLC circuit oscillates as an under-damped way:

enter image description here

I also came across the following equation:

enter image description here

As far as I understand the ωd above is the frequency of the damping oscillation (?) and ω0 is the resonant frequency which would be the oscillation freq. if the resistor was zero.

Is my way of thinking correct? If so what is ωd called in literature?

floppy380
  • 1,715
  • 7
  • 33
  • 67

1 Answers1

4

what is \$\omega_d\$ called in literature?

It's sometimes\$^{(note1)}\$ called the damped resonant frequency and applies to some 2nd order filters but not all. I regard it as the frequency where the observable resonant peak is maximum on the bode plot. For a 2nd order low pass filter this might help: -

enter image description here

The peaking frequency becomes the same as \$\omega_n\$ when there is no damping (\$\zeta\$).

For a series RLC circuit there is no difference between \$\omega_n\$ and \$\omega_d\$ - it's just the way the math turns out because there is (what is called) a "zero" at 0 Hz and this nullifies the effect of the pole situated at negative complex frequencies. If you find this last paragraph beyond your learning I do apologize.

\$^{(note1)}\$ - Often the damped resonant frequency is called the peaking frequency (as mentioned above i.e. \$\omega_d=\omega_n\sqrt{1-2\zeta^2}\$) but it is also quite often mentioned as the projection of the pole to the jw axis as per below: -

enter image description here

Note the subtle difference in the two formulas.

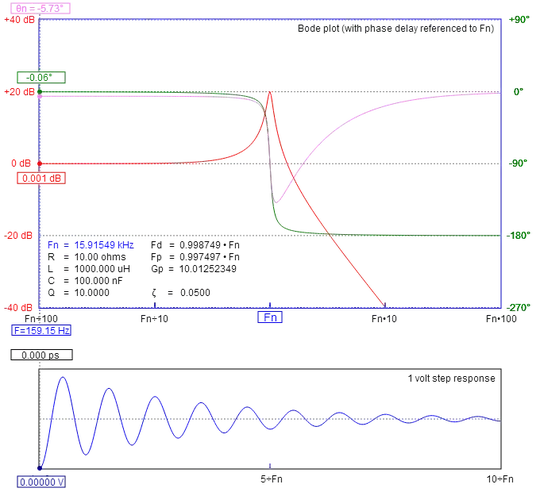
That projection to the jw axis is the frequency of the decaying oscillation as seen with a step response on (say) an RLC low pass filter like this: -

enter image description here

With values plugged-into the calculator you get a response like this (and please note the damped oscillation frequency in the lower half of the picture): -

enter image description here

On-line calculator source.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
  • Interesting that for series RLC ωd doesnt change with R and is always equal to ω0 or ωn in your terms. – floppy380 Feb 19 '18 at 13:09
  • If you understood pole zero diagrams it would make sense. – Andy aka Feb 19 '18 at 13:14
  • Here https://electronics.stackexchange.com/questions/233654/intuition-for-resonant-natural-and-oscillatory-frequencies-of-rlc-circuits they say "ωd is the damped natural frequency of the underdamped case for the series RLC circuit." and it is not equal to ω0 for RLC series circuit. See the last answer. I dont know why you say in series RLC R doesnt change ωd. Formula says the opposite. Im confused – floppy380 Feb 19 '18 at 13:21
  • @user1234 good find - the last answer is wrong... A series RLC circuit has a zero that keeps the damped frequency the same as the natural resonance. – Andy aka Feb 19 '18 at 13:28
  • It's easy to see if you think about the resonant frequency forming when inductive and capacitive reactances cancel - they are in series and that cancellation is unaffected by the added series resistance. It's mathematically trickier when you have the resistor in parallel with the capacitor for instance. – Andy aka Feb 19 '18 at 13:41
  • Yes for steady state AC that is very common sense if we think of phasors and that Xc and Xl cancels each other when Xc = Xl regardless of R. So the natural frequency is independent.. But thinking about what happens to "ωd" for a step response it is not that clear that it will result ωd = ω0. Because as you say in LP LCR filter that is not the case. – floppy380 Feb 19 '18 at 13:49