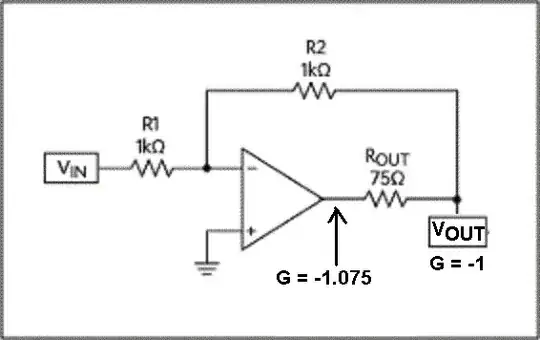
I was working a mathematical model of a non ideal op-amp circuit and I saw a slide in the following presentation:
The question I have is the following: Why does the close-loop gain \$\frac{\text{V}_\text{o}}{\text{V}_\text{i}}\$ not contain de resistor \$\text{R}_\text{o}\$?