DC analysis of common-drain NMOS amplifier

Question

The DC analysis is regarding the amplifier calculations, but that is not relevant to the topic. The equivalent DC circuit of the amplifier is:

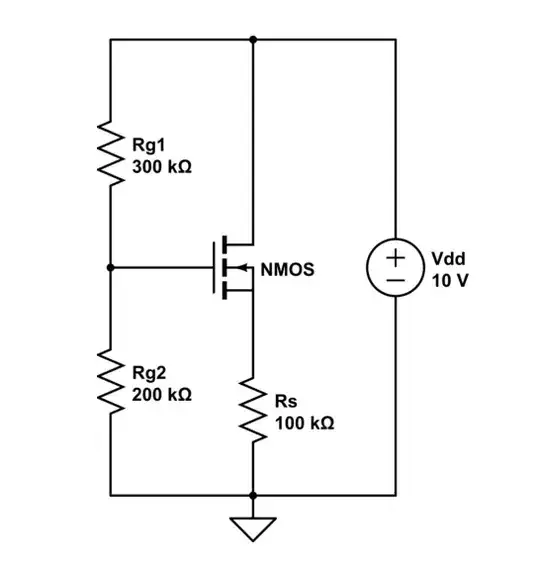
The known values are: \$R_{g1}=300\text{ k}\Omega\$, \$R_{g2}=200\text{ k}\Omega\$, \$R_s=100\text{ k}\Omega\$, \$k_n=25\ \mu\text{A/V}^2\$, \$\lambda=0.02\text{ V}^{-1}\$, \$V_{tn}=1\text{ V}\$, \$V_{dd}=10\text{ V}\$.

Now the problem is to find the bias point (drain current - \$I_D\$, voltage \$V_{GS}\$ and voltage \$V_{DS}\$).

First, I calculated the gate voltage as: $$V_G=\frac{R_{g2}}{R_{g1}+R_{g2}}V_{dd}=4\text{ V}$$ Then, I assumed that the transistor is operating in saturation mode, and set up these equations: $$I_D=k_n(V_{GS}-V_{tn})^2(1+\lambda V_{DS})$$ $$V_G=V_{GS}+R_s I_D$$ $$V_{dd}-V_{DS}-R_s I_D=0$$

The problem is, I cannot solve those equations, as there always seems to be one element missing. Any ideas on how to solve this?

@TonyStewart.EEsince'75 Actually, there are three unknowns and three equations, the first equation is just calculation of \$V_G\$. But my guess is, there is something else we could assume in this case, so the equations get a bit less complex to solve. — A6EE, Jan 31 '18 at 21:23
I can't seem to solve those three equations and there is probably something else to consider here for the equations to get more simple, but I'm not sure what. — A6EE, Jan 31 '18 at 21:30

score 1 · Accepted Answer · answered Jan 31 '18 at 21:45

For quick hand analysis, I would personally not include the impact channel length modulation.

Knowing, $$ V_{GS} = V_G - V_S\;\;\;\&\;\;\; V_{DS} = V_{dd} - V_S $$

and that the drain current equals,

$$ I_D=k_n(V_{GS}-Vtn)^2(1+\lambda V_{DS}) $$

Since gate current of Q1 is zero the drain current is also,

$$ I_D = \dfrac{V_S}{R_S} $$

Put it all together as,

$$ \dfrac{V_S}{R_S} = k_n(V_G - V_S-Vtn)^2(1+\lambda (V_{dd} - V_S)) $$ and solve for \$V_S\$.

DC analysis of common-drain NMOS amplifier

1 Answers1