But why is an opamp with single corner frequency more stable than the
one with two or more corner frequencies?
An op-amp with no break (corner) frequency (ideal) produces an open-loop phase shift of exactly 180 degrees in an inverting circuit and is inherently stable with most configurations of feedback resistors/capacitors. However, you can still turn an otherwise ideal op-amp into an oscillator by externally adding two corner frequencies. Externally generated corner frequencies behave exactly the same as internal ones; they each shift phase by 90 degrees and reduce amplitude with frequency at a higher rate.
A single break frequency shifts the open-loop phase response by 90 degrees and this means it still cannot become an oscillator when conventional negative feedback is applied because, for it to oscillate, it requires another 90 degrees to turn negative feedback into positive feedback.
Two break frequencies will inherently produce 180 degrees and quite possibly turn an inverting amplifier into an oscillator. I say this is "possible" and this is true (unless the open loop gain has fallen below unity at the point where the extra phase shift becomes 180 degrees). So you need an open-loop gain greater than unity and an added phase shift of 180 degrees to make an op-amp into an oscillator.
I read that freq. compensation is done to adjust opamp's corner freq.
to single one.
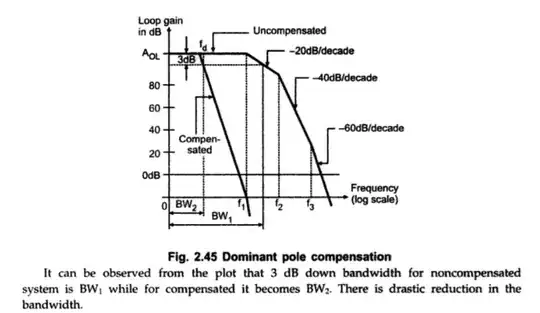
Frequency compensation can turn a previously unstable op-amp into a stable op-amp by smothering the open-loop bode plot with a corner frequency that is significantly lower than the original corner frequency in an attempt to ensure that open-loop gain drops below unity before the 2nd corner frequency is reached.
There will still be a 2nd corner frequency (and a third) but they will be at open-loop gains lees than unity. Hence they can't turn an amplifier into an oscillator.