we know probability of error of single BPSK system is \$ Q(\sqrt{\frac{2E}{N}}) \$
then what will be the probability of error when two independent identical channels are connected
and hence what will the value of \$ b \$ ?? i have proceeded like this:
since \$ P_e \$ of single BPSK system is given \$ Q( \sqrt{\gamma} \$ )
therefore \$ \gamma = \frac{2E}{N} \$ ;
now how will i proceed??
please help
i have proceeded like this:
since \$ P_e \$ of single BPSK system is given \$ Q( \sqrt{\gamma} \$ )
therefore \$ \gamma = \frac{2E}{N} \$ ;
now how will i proceed??
please help
- 145
- 2
- 15
-
2you've doubled the signal power, but the noise power only goes up by 2^0.5 – Jasen Слава Україні Jan 21 '18 at 11:00
-
Write your new gamma, extract a multiplier of the original gamma, b=sqrt(just mentioned multiplier). The multiplier is already mentioned in answers and comments. Hopefully you know that sqrt(A*B)=sqrt(A)*sqrt(B). If not, then the existence of a real problem starts to be obvious. – Jan 21 '18 at 11:57
1 Answers
For the system you have drawn (with no possible way to judge which channel is correct) if one is in error then, the probability for system error has doubled. The above is based on the confusing symbol where the two channels are recombined. I initially read it as a multiplier.
If the symbol is an adder then two BPSK signals can add and produce double the signal amplitude whereas the noise signal only goes up by \$\sqrt2\$.
Two noise sources added together can be assumed to be non-coherent hence they add as \$\sqrt{A^2+B^2}\$ hence, if A = B then the two added together increase the RMS by \$\sqrt2\$.
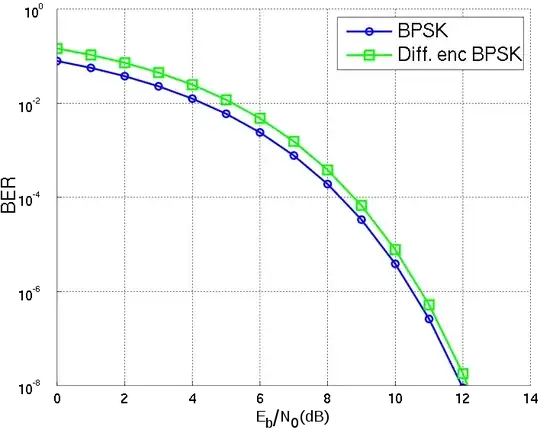
In this case the SNR (signal to noise ratio) has increased by 3 dB but, to convert this to a BER (bit error rate) means understanding what the original BER was: -
As you can see, the graph tells you the BER for a particular SNR but we don't know what the SNR was for a single channel so can't provide a definitive answer but you can use the formula you originally quoted with E/N rising by 3 dB.
- 434,556
- 28
- 351
- 777
-
-
@Jasen I understand the theory but I read the symbol shown as not an adder but a multiplier. I shall amend my answer accordingly. – Andy aka Jan 21 '18 at 11:10
-
-
1@user9198116 yes I changed my answer yesterday to coincide with that judgement. I have also added why two noise sources increase by \$\sqrt2\$ or 3 dB. – Andy aka Jan 22 '18 at 14:51
-
@Andy please help me to find the value of 'No' when noise power will go up by sqrt(2) ;where 'No/2' is the power spectral density of white Gaussian noise – Suresh Jan 23 '18 at 14:13
-
I'm unsure what you want me to do other than reiterate: If you have two unrelated noise sources of equal RMS amplitude, when you sum them, the RMS of the sum will be \$\sqrt2\$ higher than either individual noise source RMS value. – Andy aka Jan 23 '18 at 14:42
-
@Andy so according to your explanations and my formula ;Pe of this system will be Q(sqrt(2*2*E/(sqrt(2)*N))) ;which gives b=2^0.25 but answer is given as b=2^0.5 !! so what is wrong here?? – Suresh Jan 28 '18 at 06:38
-
1If we are talking about powers (rather than signals as per my answer) then signal to noise power ratio has doubled. In my answer signal to noise signal (i.e. voltage or current) has only gone up by 1.4142. – Andy aka Jan 28 '18 at 11:43
-
@Andy may you please explain the first point elaborately;i mean if we are talking about powers then how the signal to noise power ratio goes up by 2 – Suresh Jan 29 '18 at 16:20
-
1The SNR has risen by 3 dB and that is the same as doubling the power ratio. I'm not sure we are getting anywhere here. We seem to be going round in circles. Do you see why SNR goes up by 3 dB? Do you understand that to increase a signal by 3 dB means the power doubles? – Andy aka Jan 29 '18 at 16:25