Understanding of Dominant Pole Compensation

Question

According to Miller Effect, within amplifying devices such as transistors that have inverting voltage gain higher that one, there should be increased input capacitance with increased voltage gain of an amplifier.

I has been also said that this effect is limiting the amplifier at higher frequencies. This is where it comes to incorporation of a method of increasing the transistor's bandwidth. One of them is dominant pole compensation.

According to Wikipedia:

"When a capacitor is introduced between the input and output sides of the amplifier with the intention of moving the pole lowest in frequency (usually an input pole) to lower frequencies, pole splitting causes the pole next in frequency (usually an output pole) to move to a higher frequency."

I get the part when it states that 2nd pole should be moved higher in frequency (that is probably the 2nd roll-off), but why the heck would you want to decrease the 1st pole and consequently first gain roll-off begins at lower frequencies than before. What is the point of it?

I mean, shouldn't it be desired for that gain vs. frequency curve to be as flat as possible, as long as possible - to higher frequencies? But with addition of capacitor between input and output node of voltage amplifying stage, the 1st pole is decreased in frequency and at the same time that flat gain curve just became shorter then before.

I kind of get what upper plot is trying to achieve there - constant decrease of gain with increase of frequency; the straight dotted line from 1st to the 2nd roll-off of gain curve. But still, the gain is decreasing in that area, decreasing! Wouldn't it be desired to be flat as long as possible?

There are still two or three questions that are unclear to me (if some good comments are added then this post can be easily edited):

• Referring to the phase margin: Between which two points the phase shift occurs? Within negative feedback? Is it added to basic 360° shift from output of amplifier to input of negative feedback?

Also I read somewhere that the phase margin is the negative feedback to positive feedback factor. Can it be represented in such manner?

Answer 1

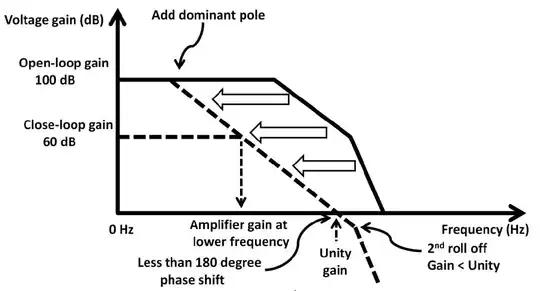
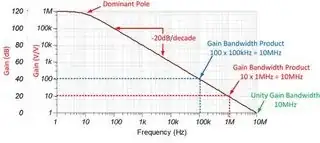
I add some comments about the phase shift.

The phase shift show here

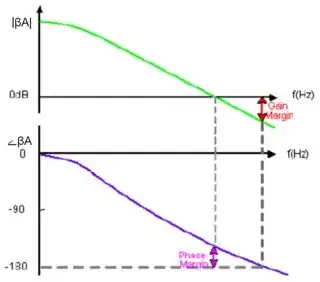
is the phase shift between the input and the output terminal of an amplifier without any feedback.

Next what you should do is to ask yourself a question what -180° really means?
It means that the voltage at the output is reversed (180° out of phase).

And now if we add a feedback network and feed back this signal to the inverting input we will receive a positive feedback amplifier ( the output voltage will start to rise).

This unwanted phase shift inside amplifier are caused by a parasitic component (capacitor or inductor). These two components provide inertia in the circuit because the electric field and magnetic field cannot change instantaneously, the time is needed. And this is why we have a phase shift in the amplifier.

And here you can see how "number" of "pole's" affect the phase shift

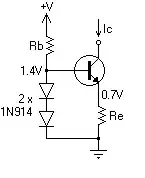
Here you can see how phase margin affects the step respond

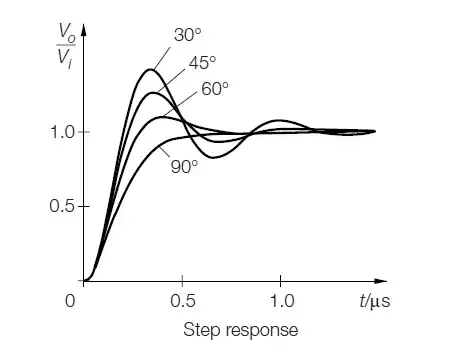
As you can see the phase margin and "circuit speed" are inversely related.

EDIT

The simplest closed loop system will look like this

Where:

\$ A \$ is open-loop gain ( forward gain )

\$\beta \$ feedback factor ( feedback network gain )

In this case \$ \beta = \frac{V_C}{V_D} = \frac{R_Y}{R_X+R_Y}\$

Based on this we can write this equation because we want to find the closed loop gain

\$A_{CL} = \frac{V_{OUT}}{V_{IN}} = \frac{V_D}{V_A}\$

So we have

\$V_D = V_B \cdot A \$ (1)

\$V_B = V_A – V_C \$ (2)

\$V_C = V_D \cdot β \$ (3)

And now we can calculate the closed loop gain, substitute 1 to 2

\$ V_D = (V_A – V_C) \cdot A = V_A \textrm{A} - V_C \textrm{A}\$ (4)

Now we take 3 (VC = VD*β) and substitute to 4

\$V_D =V_A \textrm{A} - V_C \textrm{A}= V_A\textrm{A} - V_D β \:\textrm{A} \$

\$ V_D + V_D \cdot β \cdot A = A \cdot V_A \$

\$ V_D (1 + Aβ) = A\cdot V_A\$

And finally

$$A_{CL} = \frac{V_{OUT}}{V_{IN}} = \frac{V_D}{V_A} = \frac{A}{1 + Aβ}$$

This is a very important equation. If we divide this by A we get:

$$ A_{CL} = \frac{1}{(1/A) + \beta} $$

We can see that the closed loop gain is equal to

\$\Large \frac{1}{\beta} = 1 +\frac{R_X}{R_Y}\$ do you recognizing this equation?

If the open loop gain \$A\$ is very large (ideally \$A = \infty \$) approaching infinity.

But let us back to this form

$$A_{CL} =\frac{A}{1 + Aβ}$$

This equation is true for negative feedback circuits.

And let us see what will happens if \$A\beta = 1\$ (at some frequency)

$$A_{CL} =\frac{A}{1 + Aβ} = \frac{1}{1 + 1} = 0.5$$

For negative feedback circuit.

But let us see what will happen if we add delay equal to 180 degrees phase shift at some frequency. The 180 degrees is just reversing the sign of a sinewave.

Hence, what was negative feedback became positive feedback.

Therefore \$Aβ\$ became \$-1\$

And denominator of \$A/(1+Aβ)\$ changes from sum to difference.

So the closed loop gain is \$A_{CL} =\frac{A}{1 - Aβ}\$ (positive feedback).

And again if at some frequency we have \$A\beta = 1\$

The closed loop gain becoming

$$A_{CL} =\frac{A}{1 - Aβ} = \frac{1}{ 1 - 1 } = \frac{1}{0}$$

Wow, we just create an amplifier with infinite gain even though the open-loop gain A is not infinity. This means that we can have output with zero volts at the input.

In the real world, the amplifier (with negative feedback) will oscillate at the frequency where this two contrition are met.

The magnitude of a loop gain \$A\beta(j\omega) = 1\ \$ (0dB) and the additional phase shift reaches a value of -180deg.

<----------------------------------------------------->

Also, I noticed that you have troubles with recognizing the type of a feedback in the amplifier circuits.

The Negative feedback vs Positive feedback at "DC".

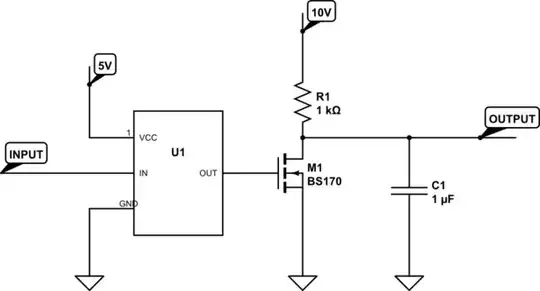
1 - Any rise in the voltage at point X will cause that the voltage at point Z also will rise.So if we connect together these two points (X and Z) we will have a Positive feedback on the circuit.

In this case (DC) the positive feedback dos not automatically means osculations. Instead of an oscillation, the circuit can latch at the positive or negative rail.

2 - This time any rise in voltage at point A corresponds to the voltage drop at point D. So, if we connect this two points together (A with D) we will end with a Negative feedback circuit.

Try is yourself.

As a homework try recognize the type of a feedback in this two circuits

The first circuit

And the second circuit

The feedback resistor is \$R_{FB}\$

Answer 2

The stability of a negative feedback amp is measured by margin to oscillation due to positive feedback. The Barkhausen stability criteria is measured at unity gain with the closed loop.

The amount of ringing in a square wave is determined by the amount of phase margin.

Each slope order -1 will add 90 deg delay so extending the flat open loop gain at the expense of adding phase shift in the closed loop at unity gain reduces the phase margin.

So the unity gain phase margin goal is >60 deg. with 90 deg being ideal maximum with 30 deg or less being a highly underdamped step response and 0 deg being an oscillator.

Thus unity gain stable Op Amps have compensation at a very low frequency so that at unity gain at max f (from GBW product), it is stable.

Meanwhile Comparators and video amps intended for high gain, do not have this compensation and are not unity gain stable with negative feedback.

Answer 3

In general, as the frequency of an amplifier's signal increases the phase lag around the loop will increase and, due to the amplifier's natural poles, the gain around the loop will decrease.

For the amplifier to be stable, the gain around the loop (Beta * Aol = feedback fraction * open loop gain) must get down below unity before the loop phase reaches 180 degrees. To get this to happen, a compensation capacitor is added to the amplifier. This is called dominant pole compensation and the size of the capacitor is chosen to roll off the open loop gain (forward gain) to ensure that the loop gain reduces to unity before the loop phase lag reaches 180 degrees. Loop gain of greater than unity with 180 degrees loop phase lag creates positive feedback and therefore an unstable amplifier.

In practice, to ensure that the amplifier is sufficiently stable, the compensation capacitor is chosen to roll the loop gain down to unity well before the loop phase reaches 180 degrees. The number of degrees between the phase at unity loop gain and 180 degrees is called the phase margin and a typical value would be 45 degrees. Loop phase of 180 degrees at unity loop gain creates what is known as a marginally stable amplifier.

The drawback of dominant pole compensation is that, as you spotted, it reduces the amplifier's bandwidth. So whilst dominant pole compensation buys you stability, it loses you open loop gain and therefore gives reduced bandwidth.

As I mentioned earlier it is the loop gain and loop phase that determine stability (phase margin).

Loop gain = open loop gain * feedback fraction = Beta * Aol

where Beta = R1/(R1+R2)

and open loop gain = (pk to pk output voltage) / (pk to pk voltage between the inputs)

So if we reduce beta (operate at a higher closed loop gain) then we can reduce the size of the compensation capacitor, lessening the severity of the dominant pole compensation, thereby increasing the open loop gain resulting in an increased bandwidth.

There are a family of op amps referred to as decompensated op amps which make use of this technique. They are guaranteed to be stable down to some minimum value of closed loop gain (5 would be an example). Thereby having an extended bandwidth. These group of op amps would be unstable if used with a closed loop gain lower than the data sheet specified minimum.

Op amps also come as an uncompensated variety. With these the size of the compensation capacitor is chosen by the design engineer to suit the closed loop gain that the amplifier is to be configured for. Thereby maximising the bandwidth. The higher the closed loop gain (lower the beta), the smaller can be the compensation capacitor giving a higher open loop gain and an increased bandwidth.

Unity gain compensated op amps have a lower bandwidth.

Its worth mentioning also that increasing the phase margin too much by increasing compensation will reduce the loop gain at every frequency. This will increase distortion and reduce other performance characteristics of the amplifier because reducing the loop gain too much reduces negative feedback. So it is also a trade off between stability and the performance characteristics of the amplifier such as distortion. This is why amplifiers are not designed for very large phase margins and 45 degrees would usually suffice.

Answer 4

If you want the maximum possible bandwidth from an amplifier, then dominant pole compensation won't give you it.

However, dominant pole compensation is a very simple, easy to specify way of getting to an amplifier that's (almost) bomb-proof. It reduces the gain to less than unity, all the while keeping the phase shift around 90 degrees. It's quite difficult to make it accidentally oscillate. It's very tolerant of the gain changing.

If you want to wrestle with and stabilise the original curve to the right, then go for it. It's possible, but you need to understand stability criteria, add several bits of lead (advance the phase shift) and to have a system with constant gain. It's usually the case that compensation for any given response that's taken down by multiple poles is sensitive to the gain. Now unfortunately the effective gain drops as a system hits the rails, so it's not unusual to have a system that's stable at small amplitude being able to keep oscillating from rail to rail. Your system has to have some means of preventing this, or returning to stability when it happens.

Answer 5

As suggested by moderator I will answer my own question, reuniting all comments and answers into one summary. If I stated anything false here then please correct me.

• The point of moving first (dominant) pole to lower frequencies is to move the second pole at the point of operation, where amplifier gain is already lower than unity. This means that if any high frequency signal (higher then the frequency of 2nd pole role-off) is somehow generated within the basic signal, it eventually fades away, because at that frequency the amplifier actually attenuates the signal rather then amplifies it. That is how stability of amplifier is achieved.

• With moving dominant pole to lower frequencies the open-loop GBW product decreased, which also means that area where function if flat (where gain is constant) got shorter (referring to upper graph). How do we achieve longer flat part of the function, where the gain of amplifier is constant? With adding negative feedback to it. With NFB network we determine the portion of that open loop signal amplitude is being fed back to differential stage, where two signals are subtracted. What is left of that open loop gain then proceeds to next stages (if there are any).

• For each added pole, the we get the phase shift of 90°, altogether 180° for two poles. Phase margin is defined as the difference of two phase shifts: from 180° (the point of second gain roll-off/ 2nd pole) to the point where GBW function crosses unity gain of 0 dB (referring to lower graph). The higher the phase margin is increased, more stable our amplifying system will become, in case of oscillations occur within it. As far as I know 90° phase margin is most optimal value for stability of system we are designing.

Sources referring to this topic:

https://en.wikipedia.org/wiki/Miller_effect#Effects

https://en.wikipedia.org/wiki/Pole_splitting

https://en.wikipedia.org/wiki/Gain–bandwidth_product

https://www.allaboutcircuits.com/technical-articles/negative-feedback-part-5-gain-margin-and-phase-margin/

http://microchipdeveloper.com/asp0107:phase-gain-margin

Op-amp dominant pole bandwidth