Constant controlled power source

Question

There are circuits for constant controlled voltage, and constant controlled current as shown below:

Voltage controlled constant current source

Voltage controlled constant voltage source

^{simulate this circuit – Schematic created using CircuitLab}

What if I wanted to create a circuit that was a voltage controlled constant power source? Here is the basic idea, I'm wondering if anyone has used a circuit that does this sort of thing, or if there are circuits that do this. I have not found any yet. I would like to control the power going into a load.

^{simulate this circuit}

Answer 1

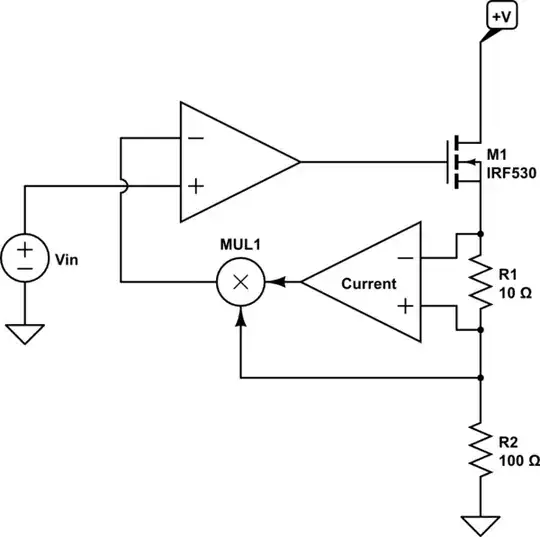
One way of doing it would be to use diodes since they have logarithmic properties.

We also know that \$P=V^2/R\$, and we also know that R will be constant (just a resistor, right?), then we can normalize our expression along these lines, \$R=1Ω\$.

This means that we can go further with this expression:

$$ \begin{align} P&=V^2/1Ω\\ P&=V^2\\ \sqrt P&=V\\ P^{1/2}&=V\\ e^{\ln(P^{1/2})}&=V\\ e^{\ln(P)/2}&=V\\ e^{(\ln(1)+\ln(P))/2}&=V\\ \\\text{Rename variables..}\\ V_{out}&=e^{(\ln(1)+\ln(V_{ref}))/2}\ \end{align} $$

Alright, we can go between \$e^x\$ and \$\ln(x)\$ with diodes, resistors and op-amps. I want to keep this answer short and concise, so rather than going in to how everything works I will show you the end result with voltages and you will hopefully be able to see how and why everything works.

Here's the link in case you want to mess around, say... change the number 3. Just scroll with your mouse button when it is over the number, or go to the right hand side and change the red "Voltage" slider.

---

The problem with this setup is the fact that the diodes have to be matched, well, you can always do some compensating with some resistors.. so it's not impossible, but it can be done purely in the analog domain.

Answer 2

Here is an application note circuit that may be useful. The power monitor chip is more economical than an analog multiplier and allows the load to be grounded, which is a big advantage in many applications.

As it says in the app note, the circuit can be scaled easily and the simple linear output stage could be replaced with a SMPS block.

The circuit controls the power to the load in parallel with the divider so it tails off a bit at high load resistances, but it's still not too shabby even at the 100mW output level.

Your circuit looks conceptually okay, concerns would include the input voltage range of the instrumentation amplifier and its common-mode rejection. Stability is the most likely thing to cause headaches in many of these circuits.

Answer 3

It is certainly possible to design a constant power source, and the schematic you posted is one approach, discussed for example here

I see in the comments that you need > 100Hz of bandwidth. Depending on the nature of the load, and range of output power if adjustable, you may have some difficulty stabilizing the loop. If the load is resistive, for example, there is highly non-linear transfer function from the output voltage (or current) to the sampled variable - i.e. the output power. That means loop gain will vary based on operating point. The problem is not intractable, though, especially if you have a well characterized load and don't need to operate over a large range of output powers.

Another option is to use an energy storage device (i.e. a capacitor or inductor) to deliver discrete, controlled energy pulses at a precise rate. It could be done with a switched capacitor or switched inductor approach, but in both cases the precision will depend on how well controlled those passives are as well as the input and output voltages. More academic, this type of solution.

Answer 4

It's certainly possible to make a constant-power source, although harder than constant voltage or constant current, especially for analog electronics. The real question is what you want it for.

To make a constant power source today, I think the easiest way is to start with a buck converter. You didn't say anything about regulation level or ripple, so a pulse on demand system would work. The processor measures the output voltage, the output current, multiplies them, then does a pulse when that is below the regulation threshold.

The electronics is the same as a normal buck converter, except for the output current sensing. The rest is firmware.

Answer 5

Constant power load i designed was composed of a dc/dc (don't remember, probably just an isolated one, but it doesn't matter) that had a constant voltage output and then a buck stage, which closed loop on current of the first dc/dc. Was very simple and way faster than 100Hz. I would guess it was around maybe 3kHz bandwidth.

Answer 6

If resistance of load is constant all what you need to control power is to control voltage over load. It is easy job of LDO.

With unknown/nonlinear load current over it should be measured. Knowing current and voltage on load power can be controlled.

One of suggestions is to use multiplier in feedback loop: https://www.edn.com/design/analog/4461981/Easy-four-quadrant-multiplier-using-a-quad-op-amp

Second way is to modulate pulses amplitude/width proportionally to voltage/current. Integration over period will give value proportional to power, and can be used in control loop.