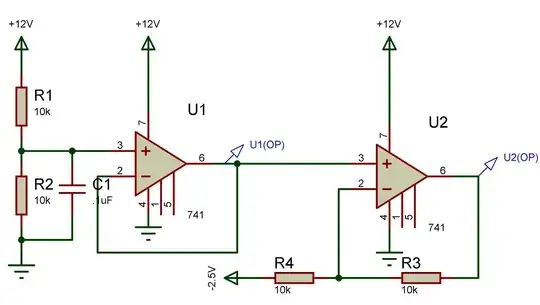
I just able to find EMF=4017 µV. Then, how can I find R1, R2, R3 and R4 with just one equation? Is my answer correct ?
Asked
Active
Viewed 127 times
-2
Jas On
- 1
- 1
-
1who on earth writes "microVolt" ?! Other than that, most basic Opamp configuration ever. Just read the Wikipedia page on Opamps and follow the link to common opamp circuits. – Marcus Müller Jan 03 '18 at 16:41
-
I'd love to help you Jas On, if you had shown at least an attempt at solving it on your own. – Harry Svensson Jan 03 '18 at 17:05
-
Hi Harry, herewith my calculation and I hope you can help me.. – Jas On Jan 03 '18 at 18:46
1 Answers
1
The overall gain of your differential amplifier must be
\begin{equation} A_V = \frac{V_o}{V_i} = \frac{1 \text{ V}}{4017 \text{ } \mu \text{V}} = 248.94 \end{equation}
Whoa, that's a lot of gain. Anyway, choosing \$ R_1 = R_3 = 1 \text{ k} \Omega \$, you need \$ R_2 = R_4 = 248.94 \text{ k} \Omega \$. That's about it.
altai
- 476
- 2
- 5
-
Thanks Altai ! You helped me. May I know whether my EMF = 4017 is correct ? I found this by trial and error or according to the equation, there are three values of EMF ? My calculator can not solve it. – Jas On Jan 03 '18 at 20:04
-
EMF = 4016.5 gives T = 99.99959 which is pretty close. There are multiple ways to find polynomial roots. Google it. – altai Jan 03 '18 at 20:11
-
Yes, I have googled it. The roots are 4017 and another two are complex roots. Thanks again for your help and apologize for the lack of my understanding. – Jas On Jan 04 '18 at 04:37
-
Hi Altai, can I ask what makes you decide to choose 1 kΩ = R1=R3 ? Can I say 100Ω = R1=R3 and 24894Ω ? Is there a way to justify which is better resistance value for this question? – Jas On Jan 05 '18 at 14:11
-
@Jas On It is for practical reasons. See the excellent top answer here: https://electronics.stackexchange.com/questions/102508/choosing-resistor-values-for-non-inverting-amplifier-and-why – altai Jan 05 '18 at 14:23