Minimizing(optimizing) digital logic circuit with multiplexer(s)

Question

(this by the way was an exam question)

For \$F = \sum m(2, 3, 5, 7, 11, 13)\$, I am trying to implement a digital logic circuit using only the following:

2:1 MUX (cost: 12, and must use at least one 2:1 MUX)
2-input AND gate (cost: 6)
2-input OR gate (cost: 6)
Inverter (cost: 2)

It obviously is pretty easy to implement it without any restrictions -- that is, if I don't care about the cost at all. But if I were to minimize the cost, how should I go about it?

I first simplified \$F\$ using the K-map of it, and I got two representations of \$F\$, \$A\$ being the MSB:

\$F = BC'D + A'B'C + B'CD + A'CD\$
\$F = BC'D + A'B'C + B'CD + A'BD\$.

The second representation just looked nice to me because I can group all the product terms by \$B\$ like this: \$F = BD(A'+C') + B'C(A'+D)\$. And apparently my design is indeed the implementation with the least cost -- I got: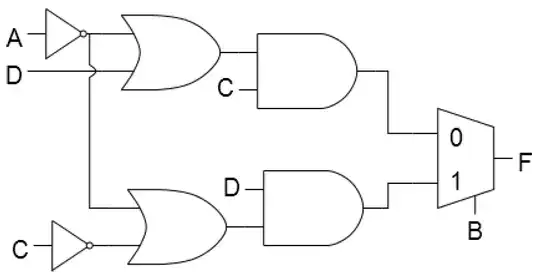

But the way I solved it cannot be used for other expressions in general, and I honestly think I just got lucky. Is there a better way to solve this problem, that is, a general way that guarantees (or at least checks) that the implementation is that of minimal cost?

Only way I know is to brute force it. Find any solution so you have an upper bound. Then go through all possible circuits with less cost and see if they have the right truth table. Output the least expensive. — Goswin von Brederlow, Jan 30 '18 at 13:13
How you will get two expressions ? The first expression is the correct one. Not the second — Mitu Raj, May 11 '18 at 10:50

score 1 · Answer 1 · answered Sep 13 '18 at 20:00

1

schematic

^{simulate this circuit – Schematic created using CircuitLab}

$34 is the best I can do. Anyone else?

answered Sep 13 '18 at 20:00

Cristobol Polychronopolis

9,622
9
17

score 0 · Answer 2 · answered Dec 21 '18 at 19:39

If you use inverters with open collector outputs you can get the cost down to about 24 without using the MUX, unfortunately in this application , the MUX is not worth its cost unless it has some other feature it adds which is not given, like HI-Z or open collector outputs, etc. It can replace one gate for a cost of 2 gates.

In real applications you could use regular inverters, since they are all internally open collector (technically drain) with a HI fanout much lower than the LO fanout. This also gives the added bonus of not spending the cost of a resistor. WARNING this use will generate a LOT of heat when the output is HI if any other parallel output is LO, but it will work and will not exceed the chips ratings on most 74 series chips.

Minimizing(optimizing) digital logic circuit with multiplexer(s)

2 Answers2