0

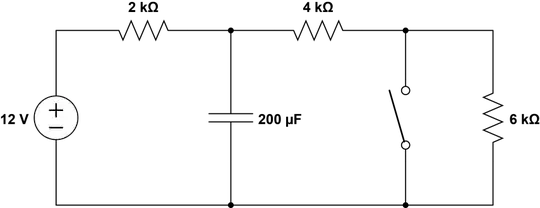
I am currently trying to find the correct measure of current through the 4KOhm Resistor in a transient response after the switch is closed.

The circuit I am supposed to simulate in Partsim

I tried to replicate the switch using AC Voltage Source with pulse.

I put in voltage in the voltage-controlled switch after 2 seconds to close

My issue seems to be that the current that PartSim is giving me doesn't match what I am expecting for the current that flows through the 4KOhm Resistor.

Currently, Partsim returns this: Current vs. Time Function Flowing Into 4KOhm Resistor

However, I thought that using the general solution, with initial current of the 4KOhm Resistor after the switch closes being 1 mA, and the final current being 2 mA, which would result in the current through the 4KOhm resistor being:

i(t) = 2-1e^(-3.75t) (RC being 4/3 KOhm)

However when I compare the two graphs (the PartSim result starting at t = 2 seconds), they don't match.

The graph based my my function: enter image description here

Could anyone please point me in the right direction as to what I am doing wrong?

Inveritatem
  • 21
  • 2
  • What is the voltage across the 4K when the switch closes? – Trevor_G Dec 26 '17 at 10:56
  • 1
    The voltage across the 4K resistor becomes 10V after the switch closes and reduces to 8V at the end. I also noticed that the voltage graph looks identical to the current graph (although the values are of course different) – Inveritatem Dec 26 '17 at 11:09
  • also, next time in PartSim instead of writing .0002 simply write 200u – G36 Dec 26 '17 at 11:11
  • I wasn't sure how to write micro, thanks for letting me know – Inveritatem Dec 26 '17 at 11:12
  • user @G36 has shown a practical way to think this. Absorb it! –  Dec 26 '17 at 11:13
  • 4 Kelvin-Ohms is not a meaningful measure of anything called a "resistor". Ping me when you fix it, and I'll undo the downvote. – Olin Lathrop Dec 26 '17 at 11:51

2 Answers2

1

Before the switch was closed the \$4\:\textrm{k}\Omega\$ resistor current was \$1 \:\textrm{m}A\$.

And the voltage across the capacitor is \$V_C = 12V \cdot \frac{4\textrm{k}\Omega + 6\textrm{k}\Omega}{2\textrm{k}\Omega + 4\textrm{k}\Omega + 6\textrm{k}\Omega} = 10V\$

Therefore after we closed the switch the initial \$4\:\textrm{k}\Omega\$ resistor current is \$ \frac{10V}{ 4\textrm{k}\Omega } = 2.5\textrm{m}A\$ And after the \$5\cdot\tau = 1.3s\$ the current will settle at \$2\textrm{m}A\$

G36
  • 13,642
  • 1
  • 18
  • 33
1

For a first order system subject to a step change, where \$x(t)\$ is the variable of interest (e.g. may be current, voltage ...), and the initial and final values and the time constant can be determined, we may use: $$ x(t)=x_{final}+\left(x_{initial}-x_{final}\right)e^{-t/\tau}$$

In this case, current through the \$\small 4\:k\Omega\$ is the variable of interest, so we have: \$i_{initial}=2.5\:mA\$, \$i_{final}=2.0\:mA\$, and \$\tau\small =(200\:\mu F\:\times\:\frac{8}{6}\:k\Omega)=0.267\:s\$, hence:

$$i(t)=2+0.5e^{-t/0.267} \:mA$$

Chu
  • 7,485
  • 2
  • 14
  • 16