Wireless channel interpretation

Question

Is there a way to estimate how fast a channel changes with respect to time in practical applications? While evaluating doppler effect for a user we use the frequency at which the channel changes. How is this frequency different from the carrier frequency we use to transmit a signal. For eg if we have a wireless system operating at 935MHz with a Bandwitdth of 2MHz and Data Rate of 2Mbps. How fast should I predict the channel to change?

Answer 1

I will just add and not repeat what the other posters have said.

If you transmit at a carrier frequency \$f_c\$ and the relative velocity between TX and RX is \$\Delta v(t)\$ then the perceived frequency deviation at the receiver at time \$t\$ (call this \$\Delta f(t)\$) will be

$$ \Delta f(t) = \frac{\Delta v(t)}{c} f_{\text{TX}} = \frac{\Delta v(t)}{c} f_c = \frac{||\Delta v(t)||}{\lambda} \cos \theta(t) = f_{\text{max}} \cos \theta (t) $$

$$ f(t) = f_c + \Delta f(t) $$

This change in receive frequency is usually called frequency dispersion and because it makes the channel sensitive to time variable \$t\$ it is said to cause time selectivity. Note that because \$\cos \theta (t) \$ will be in the interval \$[-1,1]\$, the maximum deviation is clearly \$\pm f_{\text{max}}\$, the quantity \$f_{\text{max}}\$ is the maximum doppler shift.

Now we are looking to find a particular time \$T_c\$ that would characterise how fast our channel is changing. In order words we want to find the time interval \$T_c\$ in which our channel is relatively flat so we are able to say "our channel only changes after every \$T_c\$ seconds". We want to find maximum \$T_c\$ such that:

$$ h\big(f(t)\big) \approx h\big(f(t + T_c)\big)\\ $$

or

$$ h\big(t\big) \approx h\big(t + T_c \big) $$

In order to find \$T_c\$ we first need to properly define what we mean by a channel change. If we say two channels \$h_1\$ and \$h_2\$ are different what do we actually mean? We can consider two channel responses \$h(t)\$ and \$h(t + \Delta t)\$ similar if their correlation coefficient is at least \$X\$. Where \$X\$ can be defined for any value in (0,1) but is usually taken to be either \$\frac{1}{\sqrt{2}}\$ or \$\frac{1}{2}\$.

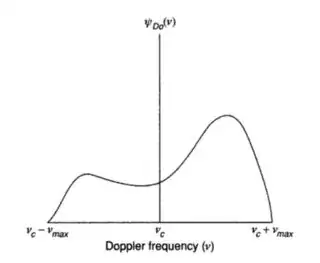
So given the speed \$(||v(t)||)\$ and arrival angle function \$(\theta (t))\$ we can compute \$T_c\$. Now, given that our wireless system is supposed to be able to support a maximum speed of say \$v_{\text{max}}\$ we usually assume \$\theta (t)\$ to be uniformly distributed between \$[0,2\pi]\$ as this is the worst case scenario. All these design variables will give us a doppler spectrum (i.e. distribution of \$f(t)\$) that looks like this:

Using the design parameters defined above and taking \$X = 0.5\$ then \$T_c\$ will be \$\approx 9/(16 \pi f_{\max})\$. This is the coherence time value that is usually reported so this is the expression you could use to estimate your coherence time.

Note that the analysis was done by taking the worst case scenario of having \$\theta (t)\$ uniformly distributed between \$[0,2\pi]\$. In practice, the spectrum will most likely be not as severe as that and the spectrum will typically be something like (image is from Introduction to Space-Time Wireless Communications by Paulraj):

Answer 2

The frequency of change of the wireless channel depends on your carrier frequency and the max speed at which your user might be moving you could assume for all ground wireless systems that the speed of a user wont exceed 10 m/s Your data rate wont affect your channel variation it only comes into effect for ISI interference

Answer 3

The Doppler effect and the rate at which the channel changes are related phenomena, but come from different effects.

Doppler

If the receiver is moving towards or away from the transmitter at a speed of V, then every one second, the distance the radio waves have to travel changes by a distance of V. This changes the apparent frequency by the ratio V/c, where c is the speed of light.

If you walk briskly at 1m/s, the V/c ratio is about 3n, or about a 3Hz Doppler shift at 935MHz. If you sit on a fast train at 100m/s, the V/c ratio rises to 300n, or a 300Hz shift at the same carrier frequency.

Rate at which the Channel Changes

Mobile radio that does not have line of sight is characterised by the radio field around the receiver being made up of very many different paths and reflections, with the signal strength being an essentially random function of position. If you move position by half a wavelength, it's likely that the peaks and troughs of the multiply reflected waves will add together significantly differently, and the signal strength there will bear no relation to that half a wavelength away, and could easily go from strong to weak, going back strong again another half wavelength away. If you only move a tiny fraction of a wavelength, the signal strength will probably stay much the same.

So a wavelength is used as a characteristic distance for one cycle of variation of this random field. Let's take a walk again. A wavelength at 935MHz is 320mm, and you would cover three of those per second at 1m/s. Although the variations you expect from the changing field are random, there are not going to change faster than this 3Hz rate. Notice the figure is exactly the same frequency as we had for the Doppler shift, so the symbol \$f_D\$ often finds its way into fading equations (the phenomenom of the signal strength varying is called fading, for obvious reasons), even though the mechanism of fading is not through Doppler. Note that moving at right angles to the line to the transmitter results in the same sort of fading result, but zero Doppler.

Data Rate

This has no effect on how fast the channel changes, only the receiver speed and carrier frequency affect that. However, for a wideband channel, different parts of the RF channel will be at a sufficiently different frequency that they fade in and out at different times, so called frequency selective fading. A narrow channel will have flat fading. Suitable channel coding, for instance OFDM, can take advantage of the frequency selective effect to obtain much more robust performance against fading than a more naive use of the channel.