I'm a computer science student and I got stuck on this question for hours.
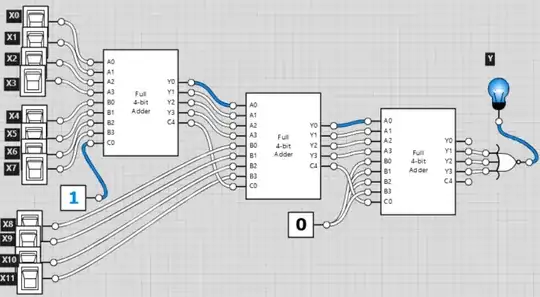
We have a binary unsigned number X, represented by 12 bits. We would like to build a system with 1 bit output - Y, that will be '1' if X is divided by 15 without a remainder.
The only components we can use are:
- 4 bit adder, having also C0 (carry) as input, and C4 as output.
- 1 single NOR gate with 3 inputs.
I did find a pattern. If I'll calculate 2^i % 15 for 0<=i<=11 (since it's 12 bits), then for I'll get a sequence 1248 1248 1248.
And if I have 0001 1110 1111 then I can just multiple all the digits, sum them, and check if my number is divisible by 15.
0 + 0 + 0 + 8 + 1 + 2 + 4 + 0 + 1 + 2 + 4 + 8 = 30
The problem is, I have no clue how to implementing it, and if it is even efficient.
I would love some help.