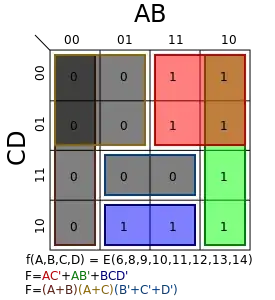
Karnaugh Map race conditions with don't cares

Question

Karnaugh maps show race conditions as adjacent minterms that are not covered in the same implicand. Take the following example:

We have race conditions when moving from the blue implicand to the green one, and the blue implicand to the red one (wrapping around the top).

My question is this: would this still apply if the adjacent '1' is a don't care, i.e. an 'X'? In this case, let's change the 1 in minterm AB'CD' (bottom right) to an 'X'. Would this still pose a potential race condition with minterm ABCD'?

Answer 1

Yes it would.

If you experience the transition A'B'CD' → AB'CD' → ABCD', the output should show 0 → X → 1, which is either 0 → 0 → 1 or 0 → 1 → 1. In both cases, you should see a single 0 → 1 transition in the output.

But with your example, you might see 0 → 1 → 0 → 1 in the output: you have a race condition.

Answer 2

An X (don't care) in the K-map means you can choose to treat that X as either a one or a zero.

In the example given, it's more convenient to treat AB'CD' as a one, otherwise you'd have to split the AB' term into AB'C' + AB'D.

So, yes, you'd have the race condition, but... Do you care if there's an output glitch when transitioning to or from a state in which you don't care what the output is? Probably in most cases, it doesn't matter.