Calculating the cut off frequency of a electronic filter

Question

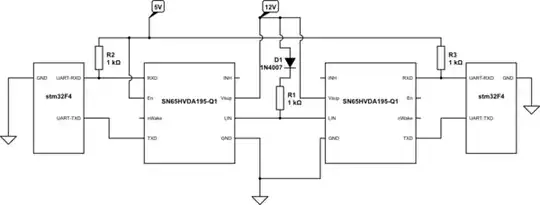
I've the following circuit:

I know that the transfer function is given by:

$$\mathscr{H}\left(\text{s}\right)=\frac{1}{1+sb_1+s^2b_2+s^3b_3}\tag1$$

Now, in this post they say that I can find the cut off frequency by finding:

$$\left|\mathscr{H}\left(\omega j\right)\right|=\frac{1}{\sqrt{2}}\cdot\left|\mathscr{H}\left(0 j\right)\right|\tag2$$

Question: so in my example I found that (when all the components have a value of \$1\$):

$$\omega_0\approx0.335005\tag3$$

Is that correct?

Thnx, but that does not answer the question :) – awwew Nov 09 '17 at 14:43 — awwew, Nov 09 '17 at 14:43

Verbal Kint · Answer 1 · 2017-11-09T18:39:14.120

3

If you replace all components values in the circuit by 1 (\$1\;\Omega\$ and \$1\;F\$) and use the equation I derived here, then the below graphs show the dynamic response and I can extract the cutoff frequency to 53 mHz or 0.335 rad/s as you correctly found.

edited Nov 09 '17 at 18:39

answered Nov 09 '17 at 18:33

Verbal Kint

20,420
1
16
50

Why do you have \$0.1\$ and \$0.053\$ Hz? – awwew Nov 09 '17 at 18:41
Ah, the 0.1 Hz value is a guess value to help Mathcad converge. The function root returns 0.053 Hz as the value for which the magnitude equals \$\frac{1}{\sqrt{2}}\$, your -3-dB cutoff frequency. – Verbal Kint Nov 09 '17 at 19:35
My pleasure if I could help. You saw how the transfer function was easily derived using the FACTs. A skill highly recommended to acquire if you work with filters. – Verbal Kint Nov 09 '17 at 19:39
I wanted to add a couple of articles from about a year back that were interesting to me: http://www.how2power.com/newsletters/1701/articles/H2PToday1701_design_ONSemi.pdf?NOREDIR=1 and also http://www.how2power.com/newsletters/1702/articles/H2PToday1702_design_ONSemi.pdf?NOREDIR=1 – jonk Nov 09 '17 at 23:09
Hi jonk, yes, these articles show the interaction of the op amp characteristics when using them in filters or compensators. This is important to account for the op amp limitations as you push the cutoff or crossover frequency. In here http://cbasso.pagesperso-orange.fr/Downloads/PPTs/Chris%20Basso%20APEC%20seminar%202015.pdf, I showed how the op amp slew-rate could affect stability in a closed-loop system. – Verbal Kint Nov 10 '17 at 09:10

score 2 · Answer 2 · answered Nov 09 '17 at 16:00

There are several definitions for the cut-off frequncy of a lowpass, depending on the specific application and on the selected approximation. But it is true that for Butterworth and Bessel responses the cut-off, in most cases, is defined at a frequency where the MAGNITUDE is 3dB down with respect to the maximum at DC. In your case, the maximim at DC is unity - and therefore the definition as given by you is correct.

The value of this cut-off frequency depends, of course, on the various parts values (which define the factors b in your transfer function). However, as no parts values are given, you cannot calculate this frequency.

(Even if all parts have the value of "1" (1 Ohm resp. 1 F), the b factors are NOT unity.)

Calculating the cut off frequency of a electronic filter

2 Answers2