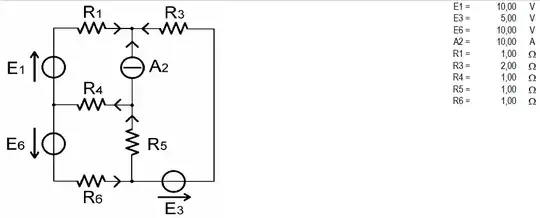
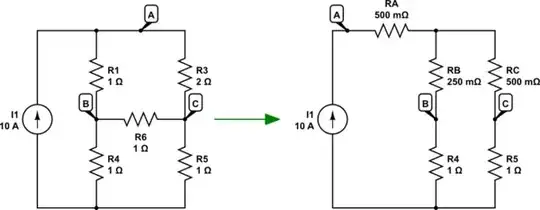
I'm trying to use superposition to solve the following linear circuit:
Step I step I considered each active component as:
But results are always wrong. Same procedure on many other circuits give me right answers, but not this one, for some obscure reason.
For example calculating I5
Step 1
Calculate parallel $$RP=\frac{(R5+R4)\cdot R6}{(R5+R4)+R6}=\frac{2\cdot 1}{2+1}=\frac{2}{3}$$ Calculate serie $$R_{tot}=R1+R3+RP=3+\frac{2}{3}=\frac{11}{3}$$ Current for the equivalent circuit (R1 and R3 current) $$I_{tot}=\frac{E1}{R_{tot}}=\frac{10}{\frac{11}{3}}=\frac{30}{11}A$$ Current for R5 $$I_{R5}=I_{tot}\cdot\frac{R6}{(R5+R4)+R6}=\frac{30}{11}\cdot\frac{1}{3}=\frac{10}{11}A$$
Step 2
Quite the same as Step 1 but with half of voltage and opposite sign $$I_{tot}=\frac{E3}{R_{tot}}=\frac{5}{\frac{11}{3}}=\frac{15}{11}A$$ Current for R5 $$I_{R5}=I_{tot}\cdot\frac{R6}{(R5+R4)+R6}=\frac{15}{11}\cdot\frac{1}{3}=\frac{5}{11}A$$
Step 3
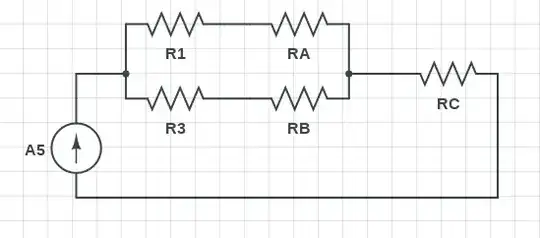
Calculate parallel $$RP=\frac{(R5+R4)\cdot (R3+R1)}{(R5+R4)+(R3+R1)}=\frac{2\cdot 3}{2+3}=\frac{6}{5}$$ Calculate serie $$R_{tot}=R6+RP=1+\frac{6}{5}=\frac{11}{5}$$ Current for the equivalent circuit (R6 current) $$I_{tot}=\frac{E6}{R_{tot}}=\frac{10}{\frac{11}{5}}=\frac{50}{11}A$$ Current for R5 $$I_{R5}=-I_{tot}\cdot\frac{(R3+R1)}{(R5+R4)+(R3+R1)}=-\frac{50}{11}\cdot\frac{3}{5}=-\frac{30}{11}A$$
Step 4
\$\Delta\$-Y conversion In circuit 3 resistors have the same value so the equivalent Y have 3 resistors of value $$\frac{1}{3}$$ Calculate parallel $$RP=\frac{(R1+RA)\cdot (R3+RB)}{(R1+RA)+(R3+RB)}=\frac{\frac{4}{3}\cdot \frac{7}{3}}{\frac{4}{3}+\frac{7}{3}}=\frac{28}{33}$$ Calculate serie $$R_{tot}=RC+RP=1+\frac{28}{33}=\frac{13}{11}$$ Current for branch RA $$I_{tot}=A5\cdot\frac{(R3+RB)}{(R1+RA)+(R3+RB)}=10\cdot\frac{\frac{7}{3}}{\frac{4}{3}+\frac{7}{3}}=\frac{70}{11}A$$
So I5 should be $$I5=\frac{10}{11}-\frac{5}{11}+\frac{30}{11}+\frac{70}{11}=\frac{105}{11}A$$
Which is wrong because of the result must be $$\frac{85}{11}A$$
The same if I consider RB branch instead of RA.
What's wrong with my procedure?