Comparator with hysteresis equations

Question

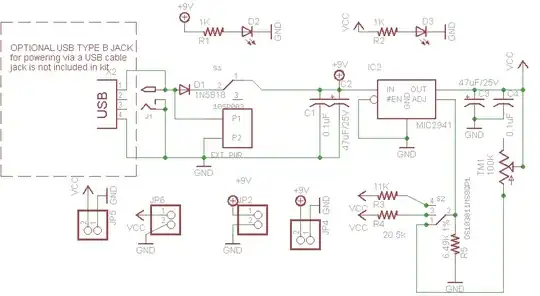
I'm trying to be sure I'm computing the values for this circuit right. Here's an example of the circuit I'm trying to build (it's going in a 12 V DC system, so I filled that in already).

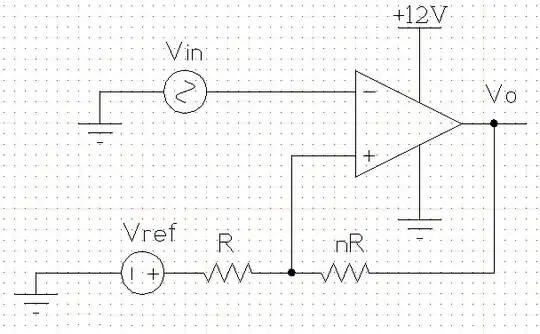
I have a textbook from electronics class several years ago (which is where the circuit design came from), and it has these formulas:

\$ V_{h}=hysteresis~width \$

\$ V_{ut}=upper~threshold~voltage \$

\$ V_{ctr}=center~of~threshold~voltages \$

\$ V_{lt}=lower~threshold~voltage \$

\$ V{ref}=comparator~reference~voltage \$

\$ n=resistor~multiplier~for~the~hysteresis~divider \$

\$ V_{h} = V_{ut}-V_{lt} \$

\$ V_{ctr}=\dfrac{V_{ut}+V_{lt}}{2} \$

\$ n=\dfrac{+V_{sat} -(-V_{sat})}{V_{h}}-1 \$

\$ V_{ref}=\dfrac{n+1}{n}V_{ctr} \$

So according to this, if I want the comparator that has V_ut = 7 V and V_lt = 6 V I should have n=11 and V_ref = 7.09 V to match my V_sat+ = 12 V and V_sat- = 0 V.

In ngspice (using an LF411 model from National Semiconductor) these values simulate an output that is more like V_ut = 7.5 V, V_lt = 6.5 V. I even used exact resistor values (R = 10 kohm, nR = 110 kohm) instead of closest-available.

Is this a good circuit to use for my purpose? Should I normally have to tweak these values for real life? I've found that R = 10 kohm, nR = 75 kohm, and V_ref = 6.5 V get me closer to the V_ut = 7 V and V_lt = 6 V that I wanted, but those values are pretty far off from expected.

Answer 1

You should see immediately that the 7.09V can't be right. 7.09V on one end of the resistors and 12V on the other end can never give you 7V on the non-inverting input. Your equation for \$V_{REF}\$ seems to be wrong.

Here's how I do it. Since the current through the resistors is the same we have

\$ \begin{cases} \dfrac{V_{SAT+} - V_{UT}}{nR} = \dfrac{V_{UT} - V_{REF}}{R} \\ \\ \dfrac{V_{SAT-} - V_{LT}}{nR} = \dfrac{V_{LT} - V_{REF}}{R} \end{cases} \$

Filling in the parameters and eliminating R:

\$ \begin{cases} \dfrac{12V - 7V}{n} = 7V - V_{REF} \\ \\ \dfrac{0V - 6V}{n} = 6V - V_{REF} \end{cases} \$

From the second equation:

\$ V_{REF} = \dfrac{n + 1}{n} 6V \$

Replacing \$V_{REF}\$ in the other equation:

\$ \dfrac{12V - 7V}{n} = 7V - \dfrac{n + 1}{n} 6V \$

We find \$n =11\$, that's also the value you found. But my \$V_{REF}\$ is different:

\$ V_{REF} = \dfrac{n + 1}{n} 6V = 6.55V \$

This is OK for a theoretical calculation, but in practice you may have a problem: do you have a 6.55V source? The typical way to solve this is to get a reference voltage via a resistor divider from your 12V power supply, and then you get this circuit:

We still have 2 equations, but three unknowns, so we can choose 1. Let's pick a 30k\$\Omega\$ for R3. Then, applying KCL:

\$ \begin{cases} \dfrac{12V - V_{UT}}{R1} + \dfrac{V_{SAT+} - V_{UT}}{R3} = \dfrac{V_{UT}}{R2} \\ \\ \dfrac{12V - V_{LT}}{R1} + \dfrac{V_{SAT-} - V_{LT}}{R3} = \dfrac{V_{LT}}{R2} \end{cases} \$

Filling in our parameters:

\$ \begin{cases} \dfrac{12V - 7V}{R1} + \dfrac{12V - 7V}{30k\Omega} = \dfrac{7V}{R2} \\ \\ \dfrac{12V - 6V}{R1} + \dfrac{0V - 6V}{30k\Omega} = \dfrac{6V}{R2} \end{cases} \$

That's

\$ \begin{cases} \dfrac{5V}{R1} + \dfrac{5V}{30k\Omega} = \dfrac{7V}{R2} \\ \\ \dfrac{6V}{R1} - \dfrac{6V}{30k\Omega} = \dfrac{6V}{R2} \end{cases} \$

From which we find

\$ \begin{cases} R1 = 5k\Omega \\ R2 = 6k\Omega \end{cases} \$

Answer 2

Assuming the comparator doesn't draw any current on its input pins, we have

i (from output of comp to Vref) = (Vo-Vref)/(R+nR). 

So V₊ (+ input comp):

V+ = (Vo-Vref)*R/(R+nR) + Vref

Which give us:

Vbottom = (Vss - Vref)*(R/(R+nR)) + Vref

And:

Vup = (Vdd - Vref)*(R/(R+nR)) + Vref

Assuming V_ss and V_dd are your negative and positive power supply. Then isolate for what you want.

Now, is it a good circuit? It depends on what you want to do and you would have to think about, in no particular order:

• Is the comparator sufficiently fast for the signal you put in.
• Is V_in a high impedance source? Because there will be some pF of parasitic capacitance to ground on the negative input of the comparator, so it might act as a low pass filter.
• Your comparator is inverting, is this really what you want? (that is, if V_in > V_up => V_o = V_ss)
• Did you provide adequate supply decoupling?
• Also, if you are abusing an op-amp as a comparator, you should be very careful, for several reason, it will be (in general) quite slow, your op-amp input common mode range might not include the range of V_in, which might cause latch-up, phase reversal and other non-specified behaviors, they might saturate and be slow to recover, etc... (see Amplifiers as comparators? for an article about abusing op-amps as comparators).