How can 4 resistors of 30ohms each be connected so you end up with a resistance of 18ohms?

Question

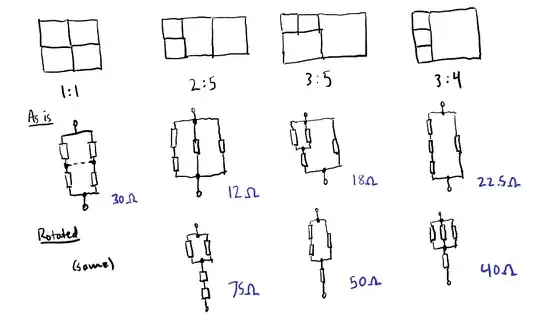
An association of 4 resistors of 30ohms each, how can one assemble them so you get a resistance equivalent of 18ohms?

Definitely not my homework, but I was doing some exercices out of curiosity and stumbled upon this one and i'm definitely stuck. — user35900, Oct 02 '17 at 15:48
there are not many combinations for 4 registers. Trying each one and calculate the resistance won't take much time — phuclv, Oct 02 '17 at 17:05
@LưuVĩnhPhúc Actually it is not that simple, and mostly a guessing game. An example of not-that-educational exercise. — Eugene Sh., Oct 02 '17 at 17:23
The answer by user43804 is by far the best. And don't VTC , this has useful answers and is on topic — Voltage Spike, Oct 02 '17 at 19:46
@J... Agreed. It's good to know Ohm's Law, but this does nothing to teach you Ohm's Law. — Graham, Oct 04 '17 at 08:05
Possible duplicate of [How do you arrange six 6-ohm resistors to have a total resistance of 6-ohm?](https://electronics.stackexchange.com/questions/105207/how-do-you-arrange-six-6-ohm-resistors-to-have-a-total-resistance-of-6-ohm) — Dmitry Grigoryev, Oct 05 '17 at 08:44
@DmitryGrigoryev These are 30 ohm resistors, not a duplicate — Voltage Spike, Oct 10 '17 at 17:09
@laptop2d So it's OK to ask the same question about e.g. 31 Ohm resistors? Or about 30 uF capacitors? — Dmitry Grigoryev, Oct 11 '17 at 07:09
@DmitryGrigoryev The questions are about a different number of resistors, which would lead to different answers. The answer is better on this one, so really you should flag the old one as a duplicate https://meta.stackexchange.com/questions/10841/how-should-duplicate-questions-be-handled I think it would be better to leave both — Voltage Spike, Oct 11 '17 at 15:43

score 71 · Answer 1 · answered Oct 02 '17 at 18:02

71

Clearly to get 18 ohms, you need some of the resistors in parallel.

So, what do you need in parallel with a 30 ohm resistor to get 18? Answer: 45 ohms.

Now, you have a simpler problem: how to make 45 ohms from three 30 ohm resistors. That should be obvious!

Some of the earlier answers have already "given you a fish," but "teaching you how to fish" is more useful in the long term IMO.

answered Oct 02 '17 at 18:02

alephzero

1,100
7
12

1

Smells pretty fishy. – Hot Licks Oct 03 '17 at 01:22
39

Or as Terry Pratchett(RIP) said: Give a man a fire and he's warm for a day, but set fire to him and he's warm for the rest of his life. – Namphibian Oct 03 '17 at 03:03
6

@Namphibian I like 21st Maxim of Maximally Effective Mercenary more ;) "Give a man a fish, feed him for a day. Take his fish away and tell him he's lucky just to be alive, and he'll figure out how to catch another one for you to take tomorrow." – Artur Biesiadowski Oct 04 '17 at 07:15
1

On the theme of "teaching him how to fish", the correct answer is "I order an 18R resistor from the E24 range". It's good to be able to calculate resistances in parallel, but this exercise is not a good way to practise that. If your book likes exercises like this, I suggest your book isn't a very good teaching resource. – Graham Oct 04 '17 at 08:07
@Graham You shouldn't create resistances like this, but you should know what happens on parallelizing and serializing resistors. – glglgl Oct 04 '17 at 08:53
I'm reluctant to resist the overwhelming capacity for bad jokes here. – Carl Witthoft Oct 04 '17 at 11:08
1

@glglgl Agreed, but a guessing game of "how many ways can you link four resistors together?" is not the way to do it. – Graham Oct 04 '17 at 13:28
I agree with @Graham, a book like this has the potential to induce bad electronics design practices in those studying from it. – Doktor J Oct 04 '17 at 15:11

Kyle Miller · Answer 2 · 2017-10-02T21:44:15.773

33

There is a technique I once found in a graph theory book by Béla Bollobás of all places. Imagine having a resistor network where the schematic can be draw without any crossings. Then for a given potential applied to the network, measure the potential and current for each component resistor. If you replace each resistor with a thin resistive plate V units tall and I units wide (V=IR so the aspect ratio is the resistance), the rectangles assemble into a single large rectangle whose aspect ratio is the equivalent resistance, and each junction shows up as a horizontal line.

This suggests a way to look for a resistor network: take four rectangles 30 units tall and 1 unit wide, and we want to find a way to scale the rectangles and assemble them into a rectangle that is 18 times taller than it is wide.

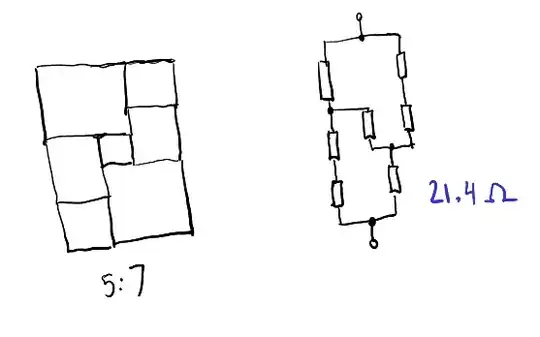
For easier visualization, since all the resistors are equal we can scale everything down vertically: the problem is to make a 18:30 (that is, 3:5) rectangle out of four squares. For illustration, I found I think every possible rectangle size and resistance you can make with these four resistors, but knowing 3:5 is the target size can speed up the search.

(Edit: I forgot 1:4, giving 7.5 and 120 Ohms.)

The equivalent resistance is 30 times the rectangle's aspect ratio. There's no need to do any sort of reduction of series/parallel circuits. An interesting bonus is that by rotating the rectangle, you get a circuit whose resistance is the reciprocal times 30 of the original circuit.

The rectangle method can be somewhat useful in the case of a network that can't be reduced using the series/parallel equations, though I think this one can be done by a delta-wye transformation:

edited Oct 02 '17 at 21:44

answered Oct 02 '17 at 19:43

Kyle Miller

451
3
6

That's a cool way to look at it :) – Thebluefish Oct 02 '17 at 20:30
3

And if you want a quick way to find the minimal network, [here it is](http://int-e.eu/~bf3/squares/view.html#30,18). – Massimo Ortolano Oct 02 '17 at 20:37
@MassimoOrtolano For when you are in that special electronics hell where all the bins in the resistor tray are labeled 1 Ohm. – Kyle Miller Oct 02 '17 at 20:57
Not 1 ohm, but [quantum Hall resistance standards](http://www.bourbaphy.fr/jeanneret.pdf) are all labeled 12.906... kohm ;-) – Massimo Ortolano Oct 02 '17 at 21:05
1

It might be slightly less surprising that this was mentioned in a book by Bollobás once you take into account that he's a Fellow of Trinity College, Cambridge, and this technique was originally developed by four undergraduate members of the Trinity Mathematical Society. Brooks, Smith, Stone, and Tutte, *The dissection of rectangles into squares*, Duke Math. J. 7 (1940) 312-340. – Peter Taylor Oct 03 '17 at 14:00
If one had a tricky network, how would one figure out what the sizes of the squares needed to be? For example, replacing one of the series pairs in your 5x7 example would yield an 11x13, but I don't know how one would figure that out except by solving the network (which seems like a cheat). – supercat Oct 04 '17 at 21:29
@supercat The size of the rectangle depends on which fraction you want to realize. In the OP, the fraction is 18/30=3/5, and so you have to tile a rectangle which is 3*5. If the you want to realize 357 ohm, you would need to tile a rectangle which is 357*18. To tile the rectangle in a minimum way, there is an exhaustive search algorithm that I linked in the comment above. Note however, that this kind of approach only yields _planar_ networks and there could be better non-planar networks. – Massimo Ortolano Oct 05 '17 at 09:10
@MassimoOrtolano: If one knows a desired resistance, that would imply the height/width ratio of the resulting rectangle. If one has a network and wants to figure out the resistance, would the "squares" technique be a practical way of doing that? How would one decide upon what size squares to use? – supercat Oct 05 '17 at 15:08
@supercat No, I daresay that is really not a practical way to solve the inverse problem of finding the resistance given the network, unless you're a fan of puzzles :-) – Massimo Ortolano Oct 05 '17 at 15:14

score 20 · Answer 3 · edited Oct 02 '17 at 16:28

20

schematic

^{simulate this circuit – Schematic created using CircuitLab}

edited Oct 02 '17 at 16:28

MatsK

738
6
15

answered Oct 02 '17 at 16:04

Trevor_G

46,364
8
68
151

calcium3000 · Answer 4 · 2017-10-02T17:48:33.343

10

Put two in parallel, trim them resistors to 18R, then throw the rest in your parts bin for later.

https://hackaday.com/2017/04/10/hackaday-trims-its-own-resistors/

Or, assuming they're 10% resistors, find the ones that are on the low end (27R) and put two in series, putting that in parallel with one 27R. Put the last one in your parts bin for later.

schematic

^{simulate this circuit – Schematic created using CircuitLab}

edited Oct 02 '17 at 17:48

answered Oct 02 '17 at 15:51

calcium3000

2,484
1
14
41

5

lol cant help thinking that is cheating – Trevor_G Oct 02 '17 at 15:52
4

I don't think it is a valid answer to this question. – Eugene Sh. Oct 02 '17 at 15:53
@EugeneSh. Fine, added another solution. Is that more valid for you? – calcium3000 Oct 02 '17 at 15:59
This one looks like more engineering, yet probably not the answer that is expected. At least show that you believe there is no mathematical answer to the stated question. – Eugene Sh. Oct 02 '17 at 16:00
5

How do you intend to trim a 30 ohm resistor down in resistance to 18 ohms? – Matt Oct 02 '17 at 16:15
@Matt Check out the HaD link. – calcium3000 Oct 02 '17 at 16:29
3

@calcium3000 I did, my question stands. You are going the wrong way in resistance for the trimming they did. – Matt Oct 02 '17 at 16:30
I guess you could trim one to 45R... LOL and keep two spares. – Trevor_G Oct 02 '17 at 16:43
@Matt Ah whoops, good catch! Someone's had a case of the Mondays. – calcium3000 Oct 02 '17 at 17:49
1

@Matt file it down, then put a thin coating of solder on it to decrease the resistance, then file the solder. Easy, right? – Grant Oct 02 '17 at 19:33

score 6 · Answer 5 · answered Oct 02 '17 at 16:03

6

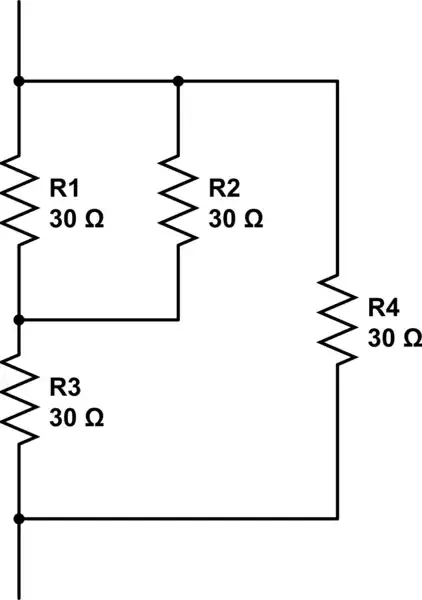
schematic

^{simulate this circuit – Schematic created using CircuitLab}

answered Oct 02 '17 at 16:03

Steve G

5,275
1
13
24

LOL Same as mine but backwards.. I guess there are two solutions. – Trevor_G Oct 02 '17 at 16:07
Cool. Didn't see this one... – Eugene Sh. Oct 02 '17 at 16:07
1

@Trevor They're identical. Each of them can be described as a 30 ohm resistor in parallel with (a 30 ohm resistor in parallel with (two 30 ohm resistors in parallel)). The same instructions build both -- 1) Take two resistors in parallel. 2) Add a third in series. 3) Connect a fourth in parallel with the first three. – David Schwartz Oct 02 '17 at 16:54
@DavidSchwartz effectively identical yes. Just laid out back asswards. – Trevor_G Oct 02 '17 at 16:55
2

@Trevor The schematics are laid out differently, but the schematic is just *showing* the solution. The solution is, per the question, a way of assembling the resistors. And both schematics depict precisely the same way of assembling the resistors. So they are not two solutions. – David Schwartz Oct 02 '17 at 16:58
@DavidSchwartz hmmm. Yes I know what you mean, but you can also argue that if top is input here, three resistors are connected to the previous stage and two connect to the next, while mine is the other way around. It's pedantic though. Also voltage at the Y connection will differ. – Trevor_G Oct 02 '17 at 17:01
@Trevor I don't think you know what I mean. You say "if top is input here" -- there is no "top" in the assembly of the resistors, only in their depiction. And the voltage at the Y connection will *not* differ unless you hook the two arrangements up differently. Two pictures of the same car depict the *same* *car* even though a different side might be on the left in each depiction and the result would be different if you did something to the side *shown* on the left in each picture. – David Schwartz Oct 02 '17 at 17:04
Yes @DavidSchwartz, I understand, but you are missing my point. In this example https://i.stack.imgur.com/ZKg76.png the network on the left is not identical to the network on the right, despite the fact that they are both 18R. – Trevor_G Oct 02 '17 at 17:14
@Trevor The two networks are identical, they're just connected into the circuit differently (one has the two-resistor junction connected to the positive, the other has the three-resistor junction connected to the positive). You can take two identical cars and if you enter the driver's side door of one something different will happen compared to entering the passenger's side door of the other. – David Schwartz Oct 02 '17 at 17:25
@DavidSchwartz yes I know.. but the left circuit has 6V at the join the other had 3V... That makes them "different". But as you say, it's just a viewpoint. – Trevor_G Oct 02 '17 at 17:30
Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/66508/discussion-between-david-schwartz-and-trevor). – David Schwartz Oct 02 '17 at 17:32

score 4 · Answer 6 · answered Oct 04 '17 at 14:58

4

take the four 30 ohms resistors back the shop and ask for an 18 ohm resistor

you might get some money back
it is quicker to wire up
is will cost less to produce
it looks neater
it will be more reliable

answered Oct 04 '17 at 14:58

Roger

59
1

score 0 · Answer 7 · answered Oct 03 '17 at 15:35

Invert the problem

Instead of seeking a resistor of 18 ohms, seek a conductor whose conductance is 1/18 siemens.

You have four conductors of 1/30 siemens.

When you parallel conductors, their conductance simply adds.

Placing conductors in series requires some fairly tricky math**, so invert them back into resistors for that math, because series resistances simply add.

** 1 / (1/C1 + 1/C2) ... Look familiar?

How can 4 resistors of 30ohms each be connected so you end up with a resistance of 18ohms?

7 Answers7

Invert the problem