Predicting thermal equilibrium: what's wrong with my time constant?

Question

I understand that this is arguably a peripheral electronics problem, but it seemed to fit here better than in physics.

I've been doing some power electronics design work with large IGBTs mounted on forced-air aluminum heat sinks. To run thermal tests, we use USB thermocouple boxes and a spreadsheet to aggregate data. It takes 30-60 minutes for most of our heat sinks to reach thermal equilibrium. Given how often we run this kind of test, I decided it would be nice to add a feature to the spreadsheet which would predict the thermal equilibrium temperature early in the procedure. If we could know where a system will level out, without having to actually wait for it to do so, it could save us days of testing.

I presume that if we could take two points along the temperature curve, we should be able to extrapolate its asymptote. Note that all temperatures are assumed to be temperatures above ambient, as we are also measuring the temperature of the air intake into the fan. My derivation is as follows:

$$ t \text{: time}\\ T(t) \text{: temperature of sink above ambient at time t}\\ Q(t) \text{: energy stored in sink}\\ P_{in}\text{: power dissipated into sink (assumed constant)}\\ T(\infty) \text{: equilibrium temperature of sink for the given power input}\\ P_{out}(t)\text{: power dissipated from sink to ambient}\\ C_{\Theta} \text{: thermal capacity of sink}\\ \tau_{\Theta} \text{: thermal time constant of sink}\\ \text{From definition: }C_{\Theta} = \frac{\Delta Q}{\Delta T} \\ \text{From definition: }R_{\Theta} = \frac{T}{P_{out}} \\ \text{At equilibrium, input power is equal to output power, so this gives:}\\ T(\infty) = R_{\Theta}P_{in} \\ \text{Energy stored is power-in minus power-out integrated over time:}\\ \Delta Q = \int_{t_1}^{t_2}(P_{in}-P_{out})dt \\ \text{Input power is constant over time, so this gives:}\\ \Delta Q = P_{in}\Delta t - \int_{t_1}^{t_2}P_{out}dt \\ \text{Substitute for output power:}\\ \Delta Q = P_{in}\Delta t - \frac{1}{R_{\Theta}}\int_{t_1}^{t_2}Tdt \\ \text{Substitute for sink energy:}\\ C_{\Theta}\Delta T = P_{in}\Delta t - \frac{1}{R_{\Theta}}\int_{t_1}^{t_2}Tdt \\ \text{Multiply by thermal resistance:}\\ R_{\Theta}C_{\Theta}\Delta T = R_{\Theta}P_{in}\Delta t - \int_{t_1}^{t_2}Tdt \\ \text{Substitute for equilibrium temperature:}\\ R_{\Theta}C_{\Theta}\Delta T = T(\infty)\Delta t - \int_{t_1}^{t_2}Tdt \\ \text{Solve for equilibrium temperature:}\\ T(\infty)=\frac{C_{\Theta}R_{\Theta}\Delta T - \int_{t_1}^{t_2}Tdt}{\Delta t} $$

So if I know the thermal resistance and capacity of the sink, I should be able to compute equilibrium temperature from two arbitrarily-chosen points on the observed temperature curve, and the integral of the data between those points. However, I've run into a problem. My equations seem to be correct, but the numbers I'm getting are totally screwy.

This particular sink weighs 10 lbs. Several websites list the specific heat capacity of aluminum as being ~.9 J/(K*g), leading to a thermal capacity of approximately 4100 J/K. We ran a test to determine the thermal resistance of the sink to ambient, by putting a fixed DC current through the IGBT packs integrated diodes and allowing the sink to come to thermal equilibrium. That gave a thermal resistance of approximately .025 K/W, for our particular combination of air flow and device layout on the sink. This gives a time constant of about 100 seconds.

Again, observations show that this sink takes nearly an hour to reach equilibrium (or at least to get so close I can't measure the difference). I'm an order of magnitude off! I have a few guesses:

1. This heat sink is not aluminum. Unlikely.
2. The thermal capacity of the sink changes with temperature. Unlikely.
3. The thermal resistance of the sink changes with temperature or some other unidentified factor, possibly the fan slowing down for some reason. More likely than the previous two, but changing by an order of magnitude still seems unlikely.
4. Input power is not constant. Vce changes with temperature, but again, not by an order of magnitude.
5. I've misplaced a decimal point. Always possible, but I can't find it.
6. I'm totally misunderstanding the entire problem.

Does anyone have an experience in this area? Any suggestions as to what I'm doing wrong?

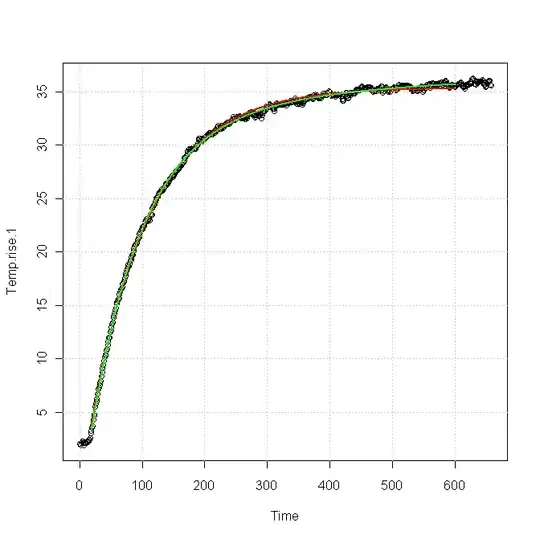
Edit: I've uploaded two example temperature curves here, for a different sink than the one I was discussing earlier. Same problems seem to occur, though.

Answer 1

Here's an alternative way to resolve your problem or figure out if your problem is physical or mathematical. Lets look at the problem from another angle and see if your measurements give the same result or a different one.

Your physical model is, you have a single heat source and a fixed path from that source to the environment, with a fixed thermal mass. Throw away all the details of the properties of aluminum, your preliminary measurement of the heat sink thermal resistance etc. With your simple (e.g. lumped-element) model, the response to turning on the heat source will be a curve like

\$T(t) = T_\infty - (T_\infty-T_0) \exp(-t/\tau)\$.

First, this shows you will need three measurements to work out the curve because you have three unknowns: \$\tau\$, \$T_\infty\$, and \$T_0\$. Of course one of these measurements can be done before the experiment starts to give you \$T_0\$ directly.

If you know \$T_0\$ and you take two measurements, you'll have

\$T_1 = T_\infty - (T_\infty-T_0) \exp(-t_1/\tau)\$

\$T_2 = T_\infty - (T_\infty-T_0) \exp(-t_2/\tau)\$

and in principle you can solve for your two remaining unknowns. Unfortunately I don't believe these equations can be solved algebraicly, so you'll have to plug them in to a nonlinear solver of some kind. Probably there's a way to do that directly in Excel, although for me it would be easier to do in SciLab, Matlab, Mathematica, or something like that.

So my point is, if you solve the problem this way, and you still get the same answer as you've already gotten, you know there is something wrong with your physical model --- an alternate thermal path, a nonlinear behavior, etc.

If you solve it this way and you get an answer that matches the physical behavior, then you know you made some algebraic or calculation error in your previous analysis. You can either track it down or just use this simplified model and move on.

Additional comment: If you do decide to just use this phenomenological model to solve your problem, consider taking more than two measurements before trying to predict the equilibrium temperature. If you have just two measurements, measurement noise is likely to cause some noticeable prediction errors. With additional measurements, you can find a least-squares solution that'll be less affected by measurement noise.

Edit Using your data, I tried two different fits:

The red curve was for a single exponential response, fitted as

\$T(t) = 33.4 - 38.6\exp(-t/81.96)\$

The green curve was for a sum of two exponentials, fitted as

\$T(t) = 36.86 - 35.82\exp(-t/81.83) - 5.42\exp(-t/383.6)\$.

You can see that both forms fit the data nearly equally for the first 100 s or so, but after about 200 s the green curve is clearly a better fit. The red curve is very nearly flattened out at the end, whereas the green curve still shows a slight upward slope, which is also apparent in the data.

I think this implies

1. You need a slightly more complex model to get a good match for your data, particularly in the tail, which is exactly what you're trying to characterize. The extra term in the model probably comes from a second thermal path out of your device.

2. It will be very difficult for a fitter to distinguish the part of the response due to the main path from the part due to the secondary path, using only, say, the first 100 s of data.

Answer 2

Quick hack.
6am. Bedtime. Must be up at 9am :-) :-(.

You will never, of course, reach thermal equilibrium - just asymptote to it until the difference meets your tolerance.

I skimmed down your formulae and nothing leaped out as wrong as far as they went, but I did not worry it to death. And I think you probably went not far enough.

The specific heat of the material will be very very very close to irrelevant.
Of relevance are the forced air convection rate as a function of delta t and air flow and somewhat secondary effects of heatsink shape and material. The latter because there will be some temperature drop getting energy out to the peripheries which is affected by geometry and material.

The following is back of an envelope without an envelope - I can't instantly convince myself you have properly covered the following, and sleep calls.

I's initially try to do Tinf without a need for summing energy in. I don't care how much energy I've put in to get to stability EXCEPT that it gives me the time taken, which is not relevant yet. Later, yes.

Tinf occurs when Power in = Power out.
You know power in.

Rate of change of Delta t will decrease as t rises as heatsink will carry off heat at an increasing rate as delta T rises. Yes? Back of back of brain says cube law, Maybe not.

Say Tinf = 70C
At 50C you have 20C driver.
If my cube law is right then
At 60 C when you have 10CV driver rate of change is 1/8th of that at 50c.
At 65C when you have 5C driver rate is 1/64th of that at 50c.
At 68C with 2C driver rate is 1/1000th of that at 50c.
At 69c it's 1/8000th

Clearly the delta that you accept for endpoint will make a vast difference for total time.

Other. At startup sink is cold. No heat out. Delta t is all conduction into thermal mass. Some rise along sink due to thermal R.
Once sink climbs above ambient by say 20C forced convection starts to bite nicely. But while output is going up due to ambient-sink delta the change of change of rate is dropping due to approaching stability as above.

This is beginning to sound shakier than I felt it to be at the start. But it's now 6:17 - I won't edit or delete etc - will post and go to sleep. See how it sounds.

Answer 3

Some areas where you could easily have an error that affects your result:

• The air flow around the part where you're testing it could be different from when you pre-measured the thermal resistance from the heat sink to ambient. If the fan speed changed, or if the airflow channel changed, or whatever, that could be a big difference.

• If the forced-air inlet temperature changed (hotter day, different lab, whatever) that will obviously affect the final temperature, and you don't mention that you measured this.

• There are other thermal paths out of your part than through the designed heat sink. Heat spreading through the ground plane of your circuit board allows your entire circuit board to act as a second heat sink. It's not as efficient as the main aluminum heat sink, but it could be changing your results. Especially if the board your using is different from the one you used when testing the heat sink.

Edit

A couple other things I can think of when we start talking about 700 W:

• The temperature of the heat sink is not strictly uniform, but you are probably measuring a single point temperature on the surface somewhere. Maybe your measurement location isn't giving you a temperature value that's representative enough to make approximations like \$C_\Theta = \Delta Q / \Delta T\$.

• If you are measuring multiple units in a single test chamber, depending on the arrangement, the heat output from one unit could be increasing the effective inlet temperatures for the downstream units.

• Thermo isn't my area, but you could be getting into an area where radiation transfer becomes significant.

Answer 4

summary

I suspect this system has 2 different time constants -- a "short" time constant close to the 100 seconds you calculated that has to do with the aluminum heat sink warming up, and some "long" time constant. Perhaps the long time constant has something to do with the chassis around the test system warming up, or for air convection cells to form, or the mass of the table it is sitting on, or something like that.

comments

To avoid confusing myself, I use "T" variables that are absolute Kelvin.

In theory, if the thermal resistance and input power were actually constant, then it would always be true that, after settling down to equilibrium,

$$ P_{in} = (T_{\infty} - T_{ambient}) / R_{\Theta} $$

for any temperature. Then you could calculate the final equilibrium temperature directly by re-arranging those terms:

$$ T_{\infty} = R_{\Theta} P_{in} + T_{ambient} $$

(This is more-or-less a simplified version of your final equation).

Alas, thermal resistance is only a linearized approximation over small differences in temperatures. Over large differences in temperature, the net radiated power (after settling to equilibrium) is proportional to the 4th power of the temperature (times the surface area times the Stefan–Boltzmann constant):

$$ P_{out} = (T_{\infty}^4 - T_{ambient}^4) A \sigma $$

As you can see from the list of thermal conductivities, the thermal conductivity of Aluminum changes significantly from 205 W/m*K at 293 K to about 250 W/m*K at 478 K. (You are right that this alone shouldn't cause an order-of-magnitude error).

In addition to radiated power, I suspect conducted power also increases faster than one might think -- at high temperatures, the heat warms up the air enough to start forming convection cells.

questions

If we could know where a system will level out, without having to actually wait for it to do so, it could save us days of testing.

Would it maybe help if you put your test system inside an insulated oven and heated it to the expected final temperature, then pulled it out for the last part of the test? Or at least turned all the fans off and threw an insulating blanket over the device under test, then yanked off the blanket and turned the fans back on for the last part of the test? The oven would warm up everything in a few seconds or a few minutes that would otherwise take nearly an hour. If the powered-up device then cools off, obviously the final temperature is below the measured temperature; if the powered-up device then heats up, the final temperature is obviously above the measured temperature -- you can decide this in less than 1 tau time constant.

Could you give us a graph of time vs. temperature -- perhaps semi-anonymized by multiplying the time scale and the temperature scale by some random constant? Then it would be easier to see if the graph was an excellent fit to a simple exponential (plus a reasonable amount of noise), or if a sum of two exponentials gives a better match.

Answer 5

Simply remind that Joule is Ws. An aluminium plate of 20x20 cm and 2mm in thickness have a mass of around 220gr, ΔT is 60oC and Power=13W. Natural cooling

So total energy will be 900 Ws/oC/g x 0,220Kg x ΔΤ = 11800 J and thermal time constant will be: tθ= 11800Ws/13W= 15min and the average charge will be about 7,5 min

If there is a thermal resistance between the plate and base Rθ = 0,1 oC/W (or 0.00025 oC/W throught) then: 0,9J/g/oC*220g = 198 J/oC and τ= 0,1*220 = 22sec

A combination of two is: τ=4*(cp/k)*ρ*Rθ^2 or 8.2min