A signal A, which is in time domain, can be transformed by Fourier transform into its frequency contents.
Then, is the signal A's frequency the highest frequency part of its Fourier transform? (i.e. is the signal itself oscillating at the frequency of its highest Fourier transform frequency part?)
Like The Photon says, it's the lowest non-zero frequency, it's called the fundamental, and the other harmonics are integer multiples of it. That means the fundamental is the frequency with the longest period in the signal.
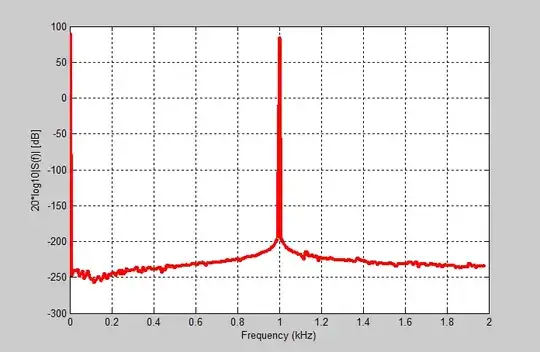
This AM signal is the product of two frequencies, a low baseband signal frequency and a higher modulating frequency, which in this case is exactly 10 times the baseband frequency. The signal's period is the lower frequency's period, and its inverse is the fundamental's frequency.
The function is (3 + sin(\$\omega_0\$)) \$\times\$ sin(\$\omega_m\$). Since
\$ sin(x) \times sin(y) = \dfrac{cos(x – y) – cos (x + y)}{2}\$
we have
\$ V_t = 3 \cdot sin(\omega_m t) + \dfrac{cos(\omega_m t - \omega_0 t)}{2} - \dfrac{cos(\omega_m t + \omega_0 t)}{2} \$
and, with \$\omega_m\$ = 10 \$\times\$ \$\omega_0\$
\$ V_t = 3 \cdot sin(10 \cdot \omega_0 t) + \dfrac{cos(9 \cdot \omega_0 t)}{2} - \dfrac{cos(11 \cdot \omega_0 t)}{2} \$
which can be written in the standard Fourier series form:
\$ V_t = -\dfrac{1}{2}sin(9 \cdot \omega_0 t - \dfrac{\pi}{2}) + 3 \mbox{ } sin(10 \cdot \omega_0 t) + \dfrac{1}{2}sin(11 \cdot \omega_0 t - \dfrac{\pi}{2}) \$
For a repeating signal the frequency of the fundamental is greater than zero, and the harmonics show in the spectrum as equal-spaced lines.
For a non-repeating signal the limit of the signal's period goes to \$\infty\$ so that the frequency of the fundamental goes to \$ \displaystyle \lim_{f \to 0} \$, and the series of harmonics forms a continuous spectrum.
I made the following observation in this answer:
"Sometimes it's difficult to see the fundamental sine in it. Take for instance the sum of a 3Hz sine and a 4Hz sine. The resulting waveform will repeat once every second, that's 1Hz. The 1Hz is the fundamental, even if its amplitude is zero. The series can be written as
\$ V_t = 0 \cdot sin(\omega_0 t) + 0 \cdot sin(2 \omega_0 t) + sin(3 \omega_0 t) + sin(4 \omega_0 t)\$
All the following terms also have zero amplitude.
Why is the fundamental frequency 1Hz,and not 0.5Hz, for instance? 3Hz and 4Hz are also multiples of that. The fundamental is the greatest common divider of the composing harmonics, and the GCD of 3 and 4 is 1. If you would choose a lower frequency its period will show a repetition of the signal, twice in the case of 0.5Hz.
A note on GCD
It has been suggested that GCD only applies to integers, like in the given example. GCD can also be applied to the rationals, however. I found that the definition \$ GCD\left(\dfrac{a}{b}, \dfrac{c}{d} \right) = \dfrac{GCD(a\cdot d, c \cdot b)}{b \cdot d} \$ seems to work, and has been confirmed to be the correct method.
Note that also in the AM example the amplitude of the fundamental is zero. The modulated signal only consists of the 9th, 10th and 11th harmonic. GCD(9 \$\omega_0\$, 10 \$\omega_0\$, 11 \$\omega_0\$) = \$\omega_0\$.
The Fourier transform gives, like you said, the "frequency contents" of the signal. The signal has content at all of the frequencies where the transform is non-zero.
If the original signal is periodic, it's Fourier transform will have characteristic spikes or peaks at the oscillation frequency of the signal and its harmonics. For example, if the signal is repetitive with frequency f, the Fourier transform will have peaks at f, 2*f, 3*f, etc. Depending on the nature of the signal, some of these peaks could be missing (for example, a pure sine wave will just show the fundamental frequency, a square wave will only have odd harmonics, etc.)
So for a periodic signal you might say that the oscillation frequency of the signal is the lowest frequency of the Fourier transform, not the highest.
Edit: As Stevenvh and Teleclavo point out, it's possible that the missing peaks include the fundamental. It's even possible for there to be many many missing peaks below the first one observed in the spectrum. For example, take a 1 Hz square wave with extremely fast rising edges (say 10 ps). Now apply a high-pass filter with cut-off at 1 GHz. Depending on how sharp is the filter, you might see no output below 10 MHz and a series of peaks at 1 Hz intervals from there up to 10 GHz, meaning the first 10 million harmonics are absent. but the repetition period remains 1 s.
And its also possible to have an aperiodic signal that has a spectrum composed of multiple peaks. My answer relates to cases where you have independent information that tells you the signal is periodic.
No. For instance the Fourier transform of a Gaussian pulse is another Gaussian pulse, neither of which appears to oscillate.
However, the opposite is true. If a signal is a sinusoidal-like oscillator, then the FT or FFT will show a spike or peak.
It is neither the lowest frequency component (of the Fourier transform) nor the highest. The Fourier transform exists even for non-periodic signals, and those signals (obviously) do not oscillate at any frequency.
I'll say even more. Even for periodic signals, it is still neither the lowest nor the highest frequency component, what -in general- determines its period. If you add two sinusoids of 19 kHz and 20 kHz (as it is commonly done in intermodulation tests for audio equipment), the spectrum has one delta at 19 kHz, and one delta at 20 kHz. However, the resulting signal has a period of 1 kHz. Neither 19 kHz, nor 20 kHz.
If you mention Fourier, forget that one signal may "oscillate" at only one frequency, and you try to see what determines the frequency of that oscillation. In general, a signal "oscillates" at infinite frequencies. All those frequencies which have nonzero component, at their Fourier transform.
Added: Even for a periodic signal, the fundamental frequency is not the one of the lowest frequency component (invisible or not) in the Fourier transform.
Take this simple example:
\$S(t)=1+sin(2\pi f_1·t)\$
with \$f_1=\$1 kHz, which looks like this:
Notice that its period is 1 ms.
Now look at the Fourier transform, S(f), of S(t):
What is the frequency of its lowest frequency component? Zero. Is f=0 the fundamental frequency of S(t)? No. The fundamental frequency of S(t) is 1 kHz.
The dominant frequency of the signal A is the one you might call it. For example a piano with 3 strings will generate 3 similar frequencies plus many complex harmonics which are typically not monotonic in strength with harmonic , not to mention phase.
So the audio of Note A0 on the piano also has harmonics of a lower magnitude on A1, A2, A3, A4 , A5, A7 and A8 and so on through all the octaves or multiples of f1 where the multiples are 1,2,3,4,5,6,7 etc
If the fundamental is dominant you call its main frequency the lowest one. But if you mute the lowest frequency say on a guitar midwave on the string or 1/4 way up the string. You suppress the fundamental and thus an overtone or harmonic is dominant so you hear that the loudest and the Fourier content on a Spectral Density meter or "Spectrum Analyzer" will prove that.
I hope this non-mathematical approach is technical enough to satisfy your curiosity.
