I have a resistive sensor, \$R_s\$ and I'd like to map the range \$700 \Omega - 1700 \Omega\$ to 0V-3.3V, ideally linearly.
Here's a circuit that does that (saturates slightly at low \$R_s\$ range):

simulate this circuit – Schematic created using CircuitLab
By applying ideal op-amp assumptions, the current through \$R_m\$ (and therefore \$R_s\$) is \$ \frac{V_{ref_1}}{R_m} \$
\$V_{o_1} = \frac{V_{ref_1}}{R_m} R_s + V_{ref_1} = V_{ref_1} (\frac{R_s}{R_m} + 1)\$
So the range at \$V_{o_1}\$ is 2.23V - 3.05V.
The second op-amp just scales this voltage range to approximately 0V-3.3V.
Other than using two op-amps, what are the downsides of this circuit?
Acoording to https://electronics.stackexchange.com/a/98395/2656, this task is possible with only one op-amp. Here is that circuit
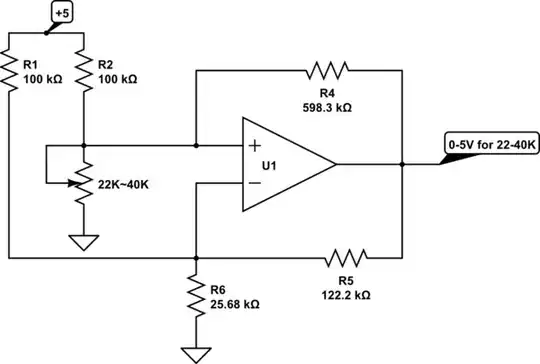
simulate this circuit (The component values correspond to a different range of voltages and resistances. Also assume that \$R_1=R_2=R_p\$. Call the sensor \$R_s\$, and instead of +5V, call it \$V_{dd}\$)
My question is: how do I analyze that circuit? I applied KCL to the two inputs of the op-amp, solved for the op-amp inputs' voltages, and set those two equal to each other, and through much messy algebra, arrived at
$$V_o = V_{dd} \frac{(R_4 R_6 - R_5 R_6 + R_4 R_5)R_s-R_4 R_5 R_6}{(R_4 R_6 - R_5 R_6 + R_p R_5)R_s-R_4 R_p R_6}$$
(V_o is not in general a linear function of R_s, however resistor values can be chosen so it is nearly linear. Perhaps there is better way to represent the transfer function so that this stands out.)
I'd like another way to reason through the circuit, perhaps relying on the symmetry of the two resistor networks at the op-amp inputs. Hopefully this way to reason about the circuit also elucidates how to choose the resistor values to map a certain resistance range to a voltage range.